Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc SAB ^ = 60°. Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:
A. πa 3 3 12
B. πa 3 2 12
C. πa 3 2 6
D. πa 3 3 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Tam giác SAB cân tại S và S A B ^ = 60 ° nên tam giác SAB đều ⇒ SA = a
![]()
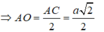
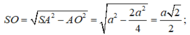
Bán kính đường tròn ngoại tiếp tứ giác ABCD là:
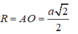
Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:
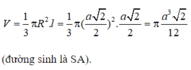

Đáp án B

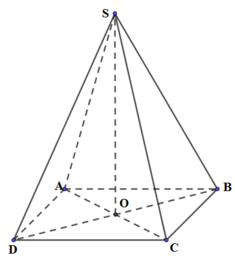
S.ABCD là chóp tứ giác đều ⇒ ABCD là hình vuông
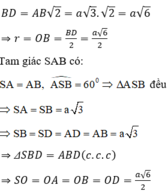
Thể tích của khối nón đỉnh S có đáy là đường tròn ngoại tiếp tứ giác ABCD:
![]()
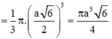

Đáp án A
Ta có: S S A B = 1 2 S H . A B = 2 a 2 ⇒ S H = 4 a
⇒ S O = S H 2 − O H 2 = 3 a 7 2
V N = 1 3 π R 2 h = 1 3 . a 2 2 . 3 a 7 2 = π a 3 7 8

Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
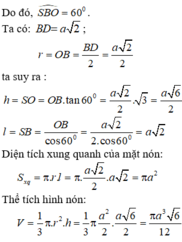
Đáp án B