Giúp mình câu 10 câu 13 14 15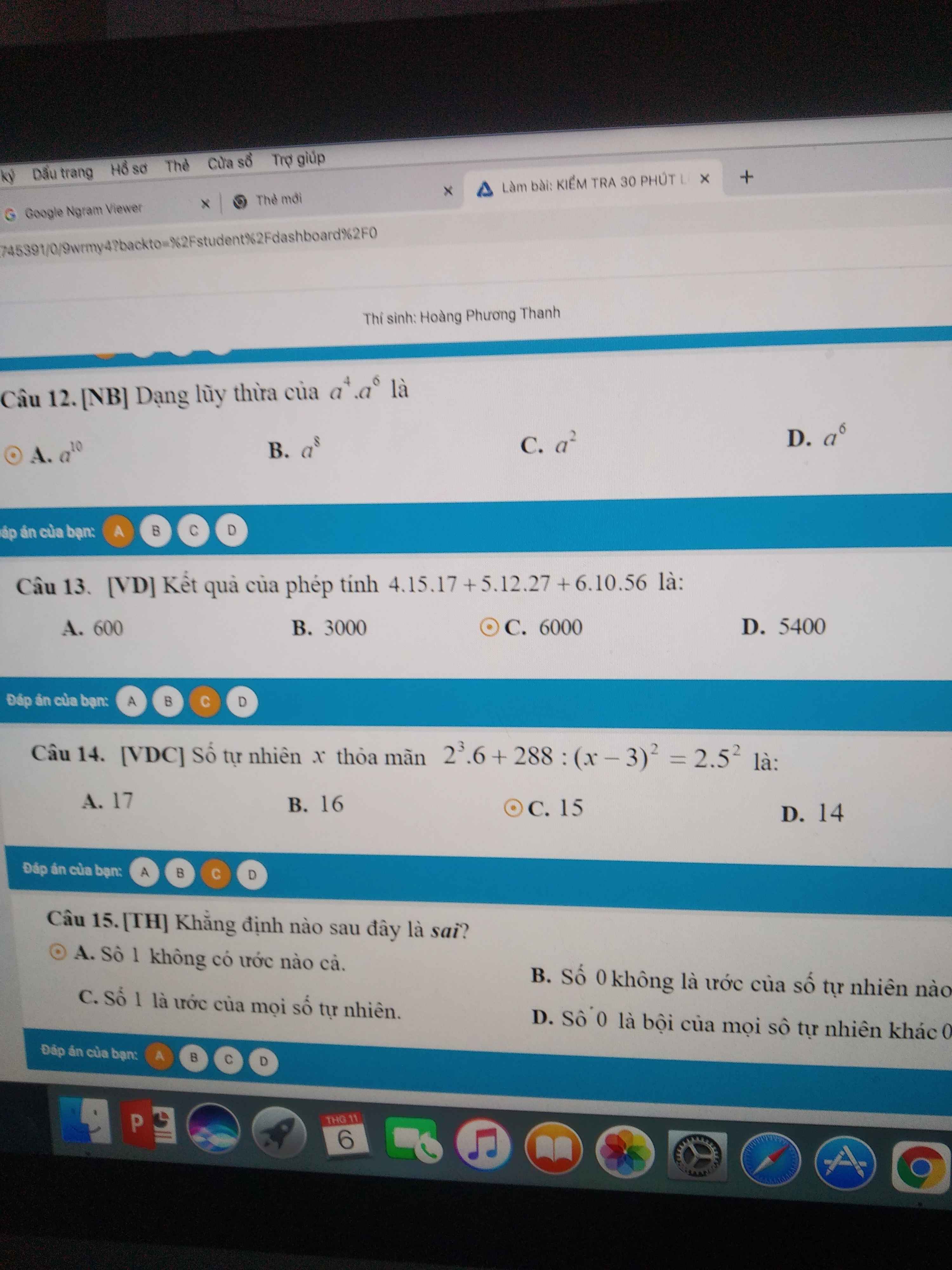
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 1
Câu 13:
1:
a: \(2x^2+2x=2x\cdot x+2x\cdot1=2x\left(x+1\right)\)
b: \(9x^2-4y^2\)
\(=\left(3x\right)^2-\left(2y\right)^2\)
=(3x-2y)(3x+2y)
2:
\(\dfrac{xy+2x+1}{xy+x+y+1}+\dfrac{yz+2y+1}{yz+y+z+1}+\dfrac{zx+2z+1}{zx+z+x+1}\)
\(=\dfrac{xy+2x+1}{\left(y+1\right)\left(x+1\right)}+\dfrac{yz+2y+1}{\left(z+1\right)\left(y+1\right)}+\dfrac{z\left(x+2\right)+1}{\left(z+1\right)\left(x+1\right)}\)
\(=\dfrac{\left(xy+2x+1\right)\left(z+1\right)+\left(yz+2y+1\right)\left(x+1\right)+\left(xz+2z+1\right)\left(y+1\right)}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{xyz+xy+2xz+2x+z+1+xyz+yz+2xy+2y+x+1+\left(xz+2z+1\right)\left(y+1\right)}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{2xyz+3xy+2xz+3x+z+2+yz+2y+x+xyz+xz+2zy+2z+y+1}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{3xyz+3xy+3xz+3yz+3x+3z+3y+3}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{3\left(xyz+xy+xz+yz+x+z+y+1\right)}{\left(xy+x+y+1\right)\left(z+1\right)}\)
=3
Câu 14:
1:
f(0)=0+5=5
2:
Vì hệ số góc của y=ax+b là -1 nên a=-1
=>y=-x+b
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3
DT
2
DN
1
28 tháng 2 2017
ban a toán lớp mấy thì toán vậy bạn có trả lời được ko mà còn ra vẻ hả bạn 'doraemi'
câu 13, 14, 15 ạ giúp em với
7 tháng 1
Câu 13:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM\cdot6=3,6^2\)
=>BM=2,16(cm)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\)
=>\(AN\cdot8=4,8^2\)
=>AN=2,88(cm)
ΔABN vuông tại A
=>\(AB^2+AN^2=BN^2\)
=>\(BN^2=2.88^2+6^2=44,2944\)
=>\(BN=\sqrt{44,2944}=\dfrac{6\sqrt{769}}{25}\left(cm\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>AH=MN=4,8(cm)
Xét ΔMBN có \(cosBMN=\dfrac{MB^2+MN^2-NB^2}{2\cdot MB\cdot MN}\)
\(=\dfrac{4,8^2+2,16^2-\dfrac{27684}{625}}{2\cdot4,8\cdot2,16}=\dfrac{-10368}{625}:\dfrac{2592}{125}=-\dfrac{4}{5}\)
=>\(sinBMN=\sqrt{1-\left(-\dfrac{4}{5}\right)^2}=\dfrac{3}{5}\)
Xét ΔBMN có \(\dfrac{NB}{sinBMN}=2R\)
=>\(2R=\dfrac{6\sqrt{769}}{25}:\dfrac{3}{5}=\dfrac{6\sqrt{769}}{25}\cdot\dfrac{5}{3}=\dfrac{2}{5}\sqrt{769}\)
=>\(R=\dfrac{\sqrt{769}}{5}\)
=>Chọn A
27 tháng 3 2022
Bài 13:
a)Môn thể thao học sinh chơi ít nhất là môn bóng rổ:
b)Số học sinh thích chơi môn bóng đá là:
900 x 35 : 100 = 315 (học sinh)
Đáp số:a) Môn thể thao học sinh chơi ít nhất là môn bóng rổ
b) 315 học sinh thích chơi môn bóng đá
Bài 4:
15,5 x 37 + 15,5 x 63
= 15,5 x (37 + 63)
= 15,5 x 100
= 1550
Bài 5:
Đáy bé là:
120 x \(\dfrac{2}{3}\) = 80 (cm)
Chiều cao là:
80 x \(\dfrac{1}{5}\) = 16 (cm)
Diện tích hình thang là:
(80 + 120) x 16 : 2 = 1600 (cm2)
Đáp số: 1600 cm2
27 tháng 3 2022
Câu 13.
a) Môn thể thao học sinh ít chơi nhất là bóng rổ với 20%
b) Số học sinh thích chơi bóng đá:
\(35\%.900=315\) (học sinh)
Đáp số: 315 học sinh thích chơi bóng đá
Câu 14.
\(15,5.37+15,5.63=15,5.(37+63)=15,5.100=1550\)
Câu 15.
Đáy bé của hình thang:
\(120.\dfrac{2}{3}=80(cm)\)
Chiều cao của hình thang:
\(80.\dfrac{1}{5}=16(cm)\)
Diện tích hình thang:
\(\dfrac{16.(80+120)}{2}=1600(cm^2)\)
Đáp số: \(1600cm^2\)
NP
4
11 tháng 3 2023
Câu 14:
\(n_{H_2O}=\dfrac{3,6}{18}=0,2\left(mol\right)\Rightarrow n_H=0,2.2=0,4\left(mol\right)\)
Có: mC + mH = 5,2 (g) ⇒ mC = 5,2 - 0,4.1 = 4,8 (g)
\(\Rightarrow n_{CO_2}=n_C=\dfrac{4,8}{12}=0,4\left(mol\right)\)
A: CnH2n-2
⇒ nA = nCO2 - nH2O = 0,4 - 0,2 = 0,2 (mol)
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_A}=2\)
→ A là C2H2.
→ Đáp án: B
Câu 15:
X: CnH2n-2
\(\Rightarrow\dfrac{2n-2}{12n+2n-2}=0,11111\Rightarrow n=4\)
→ X là C4H6.
CTCT: \(CH\equiv C-CH_2-CH_3\)
\(CH_3-C\equiv C-CH_3\)
→ Đáp án: B
13. C
14.C
15.A