Hàm số y = ( x 2 - 4 x + 3 ) π có tập xác định là
A. D = R \ { 1 ; 3 }
B. D = ( - ∞ ; 1 ) ∪ ( 3 ; + ∞ )
C. D = R
D. D = ( 0 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .


Đáp án B
+ Xét hàm y = f(x) = cos (x + π)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)
Do đó y = cos (x + π) là hàm số chẵn .
+ Xét hàm y = g(x) = tan2016x
TXĐ: D = R\{π/2 + kπ, k ∈ Z}
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan2016(-x) = (-tan x)2016 = tan2016x = g(x)
Do đó: y = tan2016x là hàm chẵn trên tập xác định của nó.
+Xét hàm y = cot2x
f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.
+ Xét hàm số y = 1-sinx
f(-x) = 1- sin(-x) = 1+ sin x
Nên hàm số không chẵn không lẻ

Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
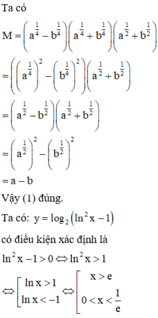
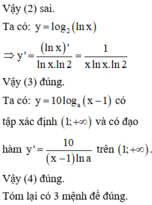

+ Xét hàm y = f x = cos x + π
TXĐ: D= R
Với mọi x ∈ D , ta có: − x ∈ D và
f − x = cos − x + π = − cos x = cos x + π = f x
Do đó y = cos x + π là hàm số chẵn trên R.
+ Xét hàm y = g x = tan 2016 x
TXĐ: D = ℝ \ π 2 + k π , k ∈ ℤ
Với mọi x ∈ D , ta có: − x ∈ D và
g − x = tan 2016 − x = − tan x 2016 = tan 2016 x = g x
Do đó: y = tan 2016 x là hàm chẵn trên tập xác định của nó
Chọn đáp án B.