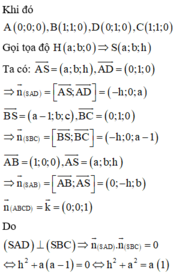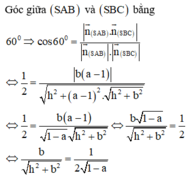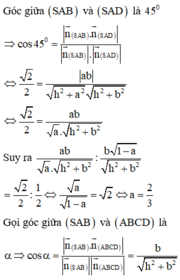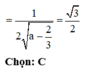Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi α là góc giữa BD và (SAD). Tính sin α
A. sin α = 6 4
B. sin α = 1 2
C. sin α = 3 2
D. sin α = 10 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi N là trung điểm AD suy ra HN // BD.
Góc giữa BD và (SAD) bằng góc giữa HN và (SAD).
Ta có AD⊥SH, AD⊥AB suy ra AD⊥ (SAB) . Trong mặt phẳng (SAB) kẻ HK⊥SA nên ta suy ra AD⊥HK và HK⊥ (SAD) . vậy góc giữa HN và (SAD) là góc HNK.
Gọi cạnh của hình vuông là a
Ta tính được HN = a 2 2 . Xét tam giác vuông SHA vuông tại H ta có
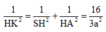
![]()
Xét tam giác vuông HNK vuông tại K ta có ![]()

Phương pháp:
- Sử dụng phương pháp tọa độ trong không gian, gắn hệ trục tọa độ gốc A và các trục tọa độ sao cho

- Sử dụng các công thức điểm, véc tơ, mặt phẳng, góc giữa hai mặt phẳng để tính toán.
Cách giải:
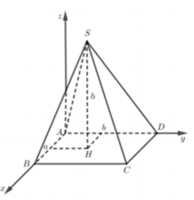
Gắn hệ trục tọa độ như hình vẽ, giả sử ABCD là hình vuông cạnh l,
chiều cao hình chóp SH = h.