Hãy vẽ hình biểu diễn của một đường tròn cùng với hai đường kính vuông góc của đường tròn đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=AC+BD

b: Xét (O) có
CA là tiếp tuyến
CM là tiếp tuyến
Do đó: CA=CM
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=AC+BD

Đáp án: D
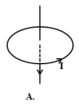
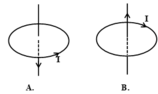
Đường sức của từ trường do dòng điện chạy trong khung dây tròn gây ra tại tâm của vòng dây có:
Điểm đặt: tại tâm vòng dây;
Phương: vuông góc với mặt phẳng chứa vòng dây;
Chiều: vào Nam ra Bắc: mặt Nam của dòng điện tròn là mặt khi nhìn vào ta thấy dòng điện chạy theo chiều kim đồng hồ, còn mặt Bắc thì ngược lại;

Đáp án D
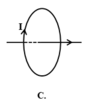
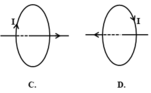
Đường sức của từ trường do dòng điện chạy trong khung dây tròn gây ra tại tâm của vòng dây có:
Điểm đặt: tại tâm vòng dây;
Phương: vuông góc với mặt phẳng chứa vòng dây;
Chiều: vào Nam ra Bắc: mặt Nam của dòng điện tròn là mặt khi nhìn vào ta thấy dòng điện chạy theo chiều kim đồng hồ, còn mặt Bắc thì ngược lại;
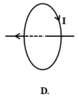
Do vậy hình D mô tả đúng quan hệ giữa chiều dòng điện và chiều của đường sức từ

Đáp án B.
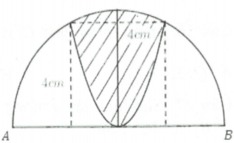
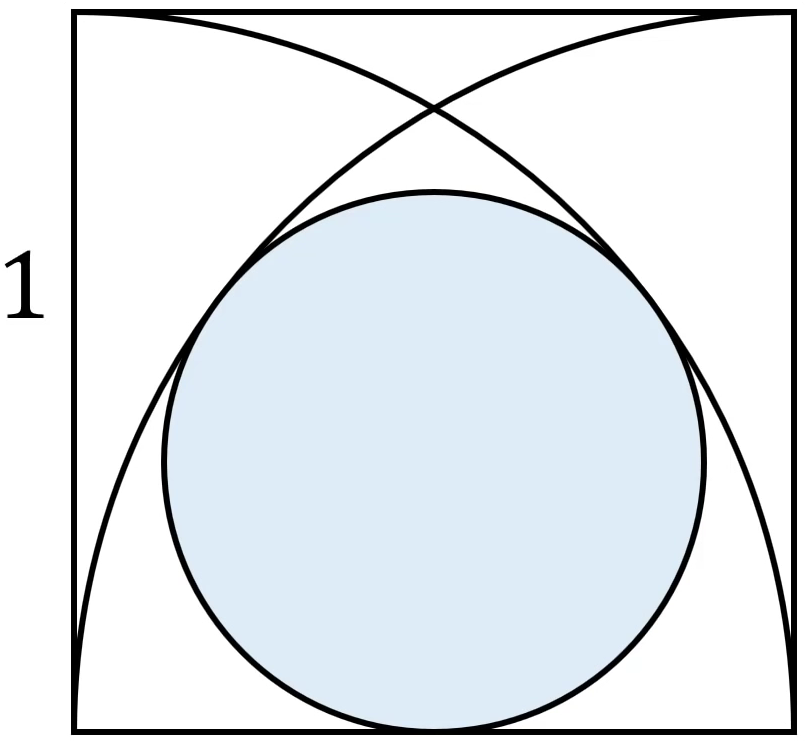
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
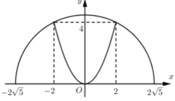
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 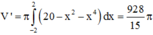
=> Thể tích cần tính 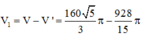
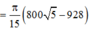



(h.2.56) Giả sử trên hình thực ta có đường tròn tâm O cùng với hai đường kính vuông góc của đường tròn đó là AB và CD. Nếu ta vẽ thêm một dây cung EF song song với AB thì đường kính CD sẽ đi qua trung điểm I của đoạn EF. Từ đó ta suy ra cách vẽ sau đây:
a) (h.2.57) Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính A'B' của hình elip đó. Đường kính này đi qua tâm O' của elip.
b) Vẽ một dây cung E'F' song song với đường kính A'B'. Gọi I' là trung điểm của E'F'. Đường thẳng O'I'cắt elip tại hai điểm C' và D'. Ta có A'B' và C'D' là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành A'C'B'D'là hình biểu diễn của hình vuông ACBD nội tiếp trong một đường tròn.