Viết (theo mẫu):
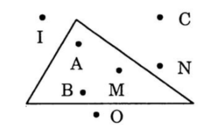
a) Các điểm ở trong hình tam giác là:
A, ………………………………….
b) Các điểm ở ngoài hình tam giác là:
I,……………………………………
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 12 2018
Phương pháp giải:
a) Quan sát hình vẽ rồi tìm ba điểm cùng nằm trên một đoạn thẳng và liệt kê theo mẫu.
b) Tô màu các tam giác thỏa mãn điều kiện của bài toán.
Lời giải chi tiết:
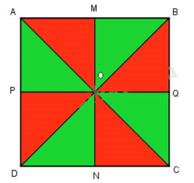
a) Viết ba điểm thẳng hàng có trong hình vẽ bên:
A, O, C;
M, O, N;
D, O, B;
A, P, D;
A, M, B;
P, O, Q;
C, Q, B;
D, N, C.
b) Tô màu các hình tam giác trong hình vẽ trên sao cho hai hình tam giác liền kề nhau có màu khác nhau.
CM
30 tháng 1 2017
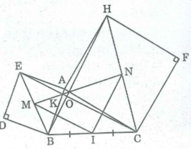
* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 11 2016
a. Ta thấy \(\widehat{EAC}=\widehat{BAH}\left(=\widehat{BAC}+90^o\right)\)
Vậy nên \(\Delta EAC=\Delta BAH\left(c-g-c\right)\)
Từ đó suy ra \(\widehat{ACE}=\widehat{AHB}\)
Vì \(\widehat{AHB}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{ACE}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{HJC}=90^o\)
Vậy \(EC\perp BH.\)
b. Ta thấy \(O_1\) là trung điểm EB. Vậy thì O1I là đường trung bình của tam giác BEC hay O1I // EC. Tương tự O2I // BH.
Lại có \(EC\perp BH\) nên \(O_1I\perp O_2I.\)
Vậy tam giác O1O2I là tam giác vuông tại I.
PT
1
PT
1
Lời giải chi tiết:
a) Các điểm ở trong hình tam giác là:
A, B, M.
b) Các điểm ở ngoài hình tam giác là:
I, C, N, O.