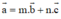Trong không gian cho ba vectơ a , b và c đều khác vectơ 0 . Khi nào ba véc tơ đó đồng phẳng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Rõ ràng a → và b → không cùng phương.
Ba vectơ a → , b → , c → đồng phẳng ⇔ ∃ cặp số ( m,n ) sao cho c → = m a → + n b →
Vì u → , v → , w → không đồng phẳng nên
x - m + n = 0 1 - 2 m - n = 0 - 2 - 3 m - n = 0 ⇔ x = - 10
Đáp án B

Đáp án C
Em có: a → , b → = 13 ; − 16 ; 2
Ba vectơ a → , b → , c → đồng phẳng thì a → , b → . c → = 0


Đáp án B.
Cách 1: Ta có
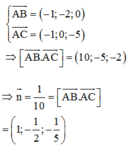
Cách 2:
Theo công thức phương trình đoạn chắn ta có phương trình
![]()
Suy ra phương trình pháp tuyến của (ABC) là
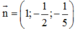
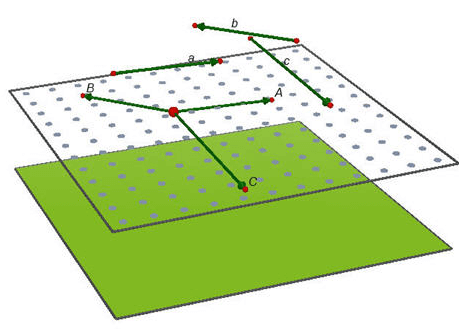



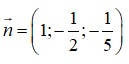

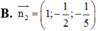

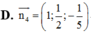
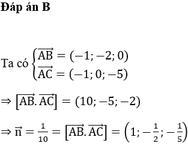
Ba vectơ a → ; b → v à c → đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:
- Giá của 3 vector đều cùng song song với mặt phẳng (P).
- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,
tức là tồn tại cặp số (m; n) duy nhất thỏa mãn