Cho hình chữ nhật ABCD có AB = 6 cm, AD = 4 cm. Điểm M nằm trên AB, MC cắt BD tại O.
c) Với AM = 2 cm.
So sánh MO với OC. Tính S A M O D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
CM
14 tháng 10 2018
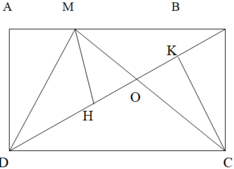
a. Nối M vơi D. Ta có S M D C = S B D C (Vì chung đay DC và chiều cao bằng chiều rộng hình chữ nhật).
Hai tam giác MDC và BDC có chung phần S O D C và có diện tích bằng nhau nên: S M D O = S B O C
b. Diện tích hình chữ nhật ABCD là ABCD
6 x 4 = 24 ( c m 2 )
Diện tích hình tam giác ADM là:
24 – 20 = 4 ( c m 2 )
Độ dài đoạn MA là:
4 x 2 : 4 = 2 ( cm )
c. Độ dài MB là:
6 – 2 = 4 ( cm )
S D M B = 2 3 S B D C (Vì đáy MB = 2 3 DC và chiều cao bằng chiều rộng của hình chữ nhật. )
Nếu coi M và C là đỉnh. Hai tam giác MBD và CBD có chung đáy BD và S M B D = 2 3 S B D C suy ra chiều cao MH = + 2 3 CK
Hai tam giác MDO và CDO có chung đáy DO và chiều cap MH = 2 3 CK
Suy ra S M D O = 2 3 S C D O
CM
3 tháng 6 2018
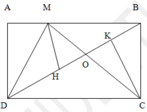
a) Nối M vơi D. Ta có S MDC = S BDC (Vì chung đay DC và chiều cao bằng chiều rộng hình chữ nhật).
Hai tam giác MDC và BDC có chung phần S ODC và có diện tích bằng nhau nên:
S MDO = S BOC
b) Diện tích hình chữ nhật ABCD là ABCD
6 x 4 = 24 ( cm2)
Diện tích hình tam giác ADM là: 4 – 20 = 4 ( cm2)
Độ dài đoạn MA là: 4 x 2 : 4 = 2 ( cm )
c) Độ dài MB là:6 – 2 = 4 ( cm )
S DMB = 2/3 S BDC (Vì đáy MB = 2/3 DC và chiều cao bằng chiều rộng của hình chữ nhật. )
Nếu coi M và C là đỉnh. Hai tam giác MBD và CBD có chung đáy BD và SMBD = 2/3 SBDC suy ra chiều cao MH = + 2/3 CK
Hai tam giác MDO và CDO có chung đáy DO và chiều cap MH = 2/3 CK
Suy ra SMDO = 2/3 SCDO
14 tháng 1 2016
A,MDO>BOC
B,hổng biết tại vì nó có thể nằm ở bất kì đâu?
C,MO<OC.Diện tích AMOD=8cm2
Tớ cũng không chắc nữa vì bài quá khó!
14 tháng 1 2016
Ai trả lời được đúng và đầy đủ tớ sẽ tick cho người đấy
HT
16 tháng 10 2020
giải
có hình
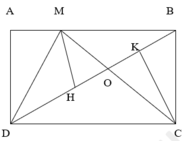
a,\(SMDC=SBCD\) ( VÌ có chung cạnh đáy DC và chung chiều cao là chiều rộng của hình chữ nhật )
\(SMOD=SBOC\) ( VÌ SMDC=SBDC và có chung phần DOC )
b, nếu \(SMBCD=20CM^2\) THÌ tổng đọ dài cạnh MB và DC của hình thang là :
20*2 : 4 = 10 ( cm2 )
Tổng độ dài cạnh AB VÀ DC LÀ :
6*2= 12 ( cm )
độ dài cạnh AM là :
12 - 10 = 2 ( cm )
c, độ dài cạch MB là : 6-2 =4 ( cm )
tỉ lệ độ dài cạnh MB và DC là : \(4:6=\frac{2}{3}\)
\(\Rightarrow\) \(SMBD=\frac{2}{3}SBCD\) ( VÌ MB = \(\frac{2}{3}\) CD và có cùng chiều cao là chiều rộng của hình chữ nhât ABCD )
\(\Rightarrow MH=\frac{2}{3}CK\) ( VÌ SMBD = \(\frac{2}{3}\) SBCD VÀ có chung cạnh đáy BD)
\(\Rightarrow SMOD=\frac{2}{3}SDOC=\frac{2}{5}MDC\) ( vì MH = \(\frac{2}{3}\) CK và có chung cạnh đáy DO )
\(\Rightarrow MO=\frac{2}{3}OC\) ( VÌ SMOD = \(\frac{2}{3}\) SOCD và có chung chiều cao hạ từ đỉnh D vuông góc với cạnh MC )
SAMD LÀ : 4*2 : 2 = 4 ( CM2 )
SMDC LÀ : 6*4 : 2 = 12 ( CM2 )
SMOD LÀ : 12 : 5 = 2,4 ( CM2 )
\(\Rightarrow\) \(SAMOD=4+2,4=6,4\left(CM2\right)\)
ĐÁP SỐ : ....