Bất phương trình bậc nhất một ẩn có dạng như thế nào? Cho ví dụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
3
LS
22 tháng 4 2017
Bất phương trình bậc nhất một ẩn có dạng: ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a, b là hai số đã cho, a ≠ 0.
Ví dụ: 2x + 4 < 0 (hoặc 2x + 4 > 0, 2x + 4 ≤ 0, 2x + 4 ≥ 0)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Ví dụ:
\(\begin{array}{l}{x^2} - x + 1 > 0\\ - {x^2} + 5x + 5 \le 0\end{array}\)
b)
Bất phương trình bậc nhất: \(x - 1 > 0\)
Bất phương trình hai ẩn: \(2x + y < 5\)
7 tháng 3 2022
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
KV
10 tháng 5 2023
a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c)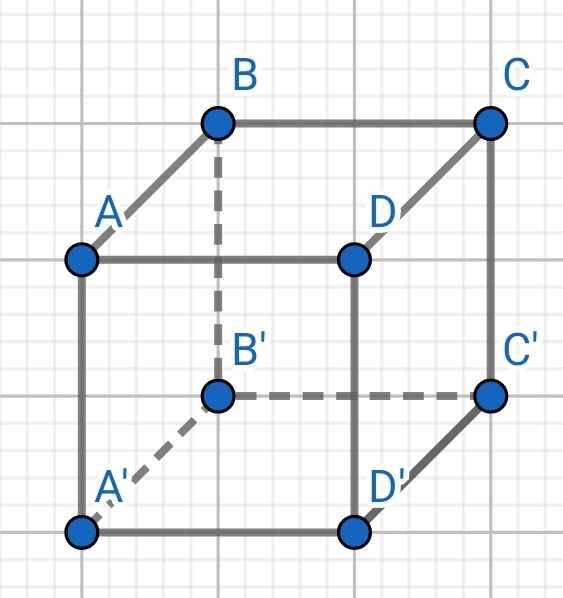 
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
10 tháng 5 2023
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3
CM
19 tháng 9 2018
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ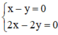 
và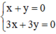 
Hệ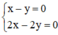 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ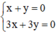 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
CM
8 tháng 6 2019
2x + 3 ≥ -6
Vế trái của bất phương trình: 2x + 3
Vế phải của bất phương trình: -6
CM
8 tháng 2 2017
- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.
- Bạn Phương nhận xét sai.
Ví dụ: Xét hai hệ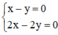 
và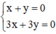 
Hệ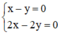 
có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.
Hệ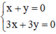 
có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.
Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.
Kiến thức áp dụng
Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
Bất phương trình bậc nhất một ẩn có dạng: ax + b < 0 (hoặc ax + b > 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a, b là hai số đã cho, a ≠ 0.
Ví dụ: 2x + 4 < 0 (hoặc 2x + 4 > 0, 2x + 4 ≤ 0, 2x + 4 ≥ 0)