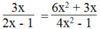Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
A 2 x - 1 = 6 x 2 + 3 x 4 x 2 - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

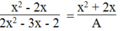 ⇒
x
2
-
2
x
.
A
=
2
x
2
-
3
x
-
2
x
2
+
2
x
⇒
x
2
-
2
x
.
A
=
2
x
2
-
3
x
-
2
x
2
+
2
x
⇒ x x - 2 . A = 2 x 2 - 4 x + x - 2 . x x + 2
⇒ x x - 2 . A = 2 x x - 2 + x - 2 . x x + 2
⇒ x(x – 2).A = (x – 2)(2x + 1).x.(x + 2)
⇒ A = (2x + 1)(x + 2) = 2 x 2 + 4 x + x + 2 = 2 x 2 + 5 x + 2
Vậy 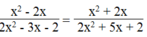

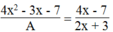 ⇒
4
x
2
-
3
x
-
7
2
x
+
3
=
A
4
x
-
7
⇒
4
x
2
-
3
x
-
7
2
x
+
3
=
A
4
x
-
7
⇒ 4 x 2 + 4 x - 7 x - 7 2 x + 3 = A 4 x - 7
⇒ [4x(x + 1) – 7(x + 1)](2x+ 3) = A(4x - 7)
⇒ (x + 1)(4x – 7)(2x + 3) = A(4x – 7)
⇒ A = (x + 1)(2x + 3) = 2 x 3 + 3 x + 2 x + 3 = 2 x 2 + 5 x + 3
Vậy 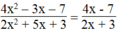

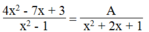 ⇒
4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒
4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒ 4 x 2 - 4 x - 3 x + 3 x + 1 2 = A x + 1 x - 1
⇒ 4 x x - 1 - 3 x - 1 . x + 1 2 = A . x + 1 x - 1
⇒ x - 1 4 x - 3 x + 1 2 = A x + 1 x - 1
⇒ A = 4 x - 3 x + 1 = 4 x 2 + 4 x - 3 x - 3 = 4 x 2 + x - 3
Vậy 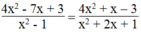

\(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\)
\(\Rightarrow A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}\)
\(\Rightarrow A=\dfrac{-\left(3-x\right)\left(y-x\right)}{3-x}\)
\(\Rightarrow A=x-y\)
_____
\(\dfrac{5x}{x+1}=\dfrac{Ax\left(x+1\right)}{\left(1-x\right)\left(1+x\right)}\)
\(\Rightarrow A=\dfrac{5x\left(x+1\right)\left(1-x\right)}{x\left(x+1\right)}\)
\(\Rightarrow A=5\left(1-x\right)\)
\(\Rightarrow A=5-5x\)
____
\(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\)
\(\Rightarrow\dfrac{\left(4x-1\right)\left(x-1\right)}{A}=\dfrac{4x-1}{x+3}\)
\(\Rightarrow A=\dfrac{\left(4x-1\right)\left(x-1\right)\left(x+3\right)}{4x-1}\)
\(\Rightarrow A=\left(x-1\right)\left(x+3\right)\)
\(\Rightarrow A=x^2+2x-3\)
⇒ A(2x – 1)(2x + 1) = (2x – 1).3x(2x + 1) ⇒ A = 3x
Vậy