Lập phương trình mặt phẳng (P) chứa hai đường thẳng: d: x = - 2 - t y = 1 + 4 t z = 1 - t và d': x = - 1 + t ' y = - 3 + 4 t ' z = 2 - 3 t '
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 1 2017
Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương là a → (−1; 4; −1)
Đường thẳng d1 đi qua N(1; 1; 1) có vecto chỉ phương là b → (1; 4; −3)
Ta có: MN → (3; 0; 0); a → ∧ b → = (−8; −4; −8) nên MN → ( a → ∧ b → ) ≠ 0, suy ra d và d 1 chéo nhau. Do đó (P) là mặt phẳng đi qua M(-2; 1; 1) có vecto pháp tuyến bằng a → ∧ b →
Phương trình của (P) là: –8(x + 2) – 4(y – 1) – 8(z – 1) = 0 hay 2x + y + 2z + 1 = 0
CM
15 tháng 6 2019
Đáp án A
Đường thẳng d 1 đi qua A(1; 1; 1), vecto chỉ phương u 1 → (1; 0; -1)
Đường thẳng d 2 đi qua B( 0; 2;1), vecto chỉ phương u 2 → (-1; 1; 0)
Mặt phẳng (P) chứa hai đường thẳng d 1 ; d 2 nên nhận vecto [ u 1 → ; u 2 → ] = (1;1;1) làm vecto pháp tuyến và đi qua A(1;1;1). Phương trình (P):
1(x - 1) + 1(y – 1) + 1(z - 1) = 0 hay x + y + z – 3= 0
Chọn A.
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
a.
Chọn \(C\left(1;1;1\right)\) là 1 điểm thuộc denta
\(\Rightarrow\overrightarrow{AC}=\left(0;-1;4\right)\)
Đường thẳng denta có \(\overrightarrow{u_{\Delta}}=\left(2;-1;1\right)\) là 1 vtcp
\(\Rightarrow\left[\overrightarrow{AC};\overrightarrow{u_{\Delta}}\right]=\left(3;8;2\right)\)
\(\Rightarrow\left(Q\right)\) nhận \(\left(3;8;2\right)\) là 1 vtpt
Phương trình (Q):
\(3\left(x-1\right)+8\left(y-2\right)+2\left(y+3\right)=0\)
b.
Mặt phẳng (P) nhận \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) là 1 vtpt
Ta có: \(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_{\left(P\right)}}\right]=\left(-2;-1;3\right)\)
Mặt phẳng (Q) nhận (2;1;-3) là 1 vtpt
Phương trình (Q):
\(2\left(x-1\right)+1\left(y-2\right)-3\left(z+3\right)=0\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
c.
Gọi M là giao điểm denta và (P) thì tọa độ M thỏa:
\(-1+2t+2-t+t-3=0\Rightarrow t=1\)
\(\Rightarrow M\left(1;1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{u_{\Delta}}\right]=\left(2;1;-3\right)\)
Đường thẳng d nhận (2;1;-3) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=1+t\\z=1-3t\end{matrix}\right.\)
d.
Do M thuộc denta nên tọa độ có dạng: \(M\left(-1+2t;2-t;t\right)\)
M là trung điểm AN \(\Rightarrow N\left(-3+4t;2-2t;2t+3\right)\)
N thuộc (P) nên: \(-3+4t+2-2t+2t+3-3=0\Rightarrow t=\dfrac{1}{4}\)
\(\Rightarrow\overrightarrow{MN}=\left(-2+2t;-t;t+3\right)=\left(-\dfrac{3}{2};-\dfrac{1}{4};\dfrac{13}{4}\right)=-\dfrac{1}{4}\left(6;1;13\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=1+6t\\y=2+t\\z=-3+13t\end{matrix}\right.\)
CM
26 tháng 10 2018
Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương a → (−1; 4; −1)
Ta có: MI → (1; −2; 0), chọn n P → = MI → ∧ a → = (2; 1; 2)
Phương trình của (P) là: 2(x + 2) + (y – 1) + 2(z – 1) = 0 hay 2x + y + 2z + 1 = 0
CM
21 tháng 2 2017
(β) vuông góc với d
⇒ (β) nhận vtcp của d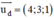 
là 1 vtpt.
(β) đi qua M(0; 0; -2)
⇒ (β): 4x + 3y + z + 2 = 0.
CM
9 tháng 8 2018
Chọn B
Mặt cầu (S) có tâm I (3;1;0) và bán kính là R = 2.
Gọi H (1+2t;-1+t;-t) là hình chiếu của I trên d.
Gọi (Q) là mặt phẳng chứa d.
Bán kính đường tròn giao tuyến của mặt phẳng chứa d và mặt cầu (S) là 
, suy ra r nhỏ nhất khi d (I, (Q)) lớn nhất.
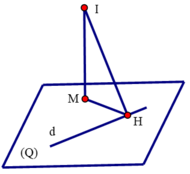
Gọi M là hình chiếu của I trên (Q).
Ta có d (I, (Q)) = IM ≤ IH suy ra d (I, (Q)) lớn nhất khi d (I, (Q)) = IH, lúc đó mặt phẳng (Q) qua H (3;0;-1) và có một véc tơ pháp tuyến là 
Phương trình mặt phẳng (Q): y+z+1=0.
CM
30 tháng 10 2019
Đáp án D.
Ta dễ thấy hai đường thẳng d và d ' song song.
Hai đường thẳng d và d ' lần lượt đi qua hai điểm M 5 ; 1 ; 5 và N 3 ; − 3 ; 1 và có vtcp u → = 2 ; − 1 ; 1 . Ta có M N → = − 2 ; − 4 ; − 4 .
Hai vecto M N → và u → không cùng phương và có giá nằm trên mặt phẳng P nên ta có vtpt của mặt phẳng P là n → = M N → ; u → .
Ta tìm tọa độ của n → bằng MTCT:
⇒ n → = − 8 ; − 6 ; 10
Mặt phẳng P có vtpt n → = − 8 ; − 6 ; 10 và đi qua M 5 ; 1 ; 5 nên có phương trình P : − 8 x − 5 − 6 y − 1 + 10 z − 5 = 0 ⇔ P : 4 x + 3 y − 5 z + 2 = 0 .Ta chọn D.
Đường thẳng d đi qua M(-2; 1; 1) có vecto chỉ phương là a → (−1; 4; −1)
Đường thẳng d’ đi qua N(-1; -3; 2) có vecto chỉ phương là b → (1; 4; −3)
Suy ra: a → ∧ b → = (−8; −4; −8) ≠ 0 →
Ta có: MN → (1; −4; 1) nên MN → .( a → ∧ b → ) = 0 do đó hai đường thẳng d và d’ cắt nhau.
Khi đó (P) là mặt phẳng đi qua M(-2; 1; 1) và có n P → = (2; 1; 2)
Phương trình của (P) là : 2(x + 2) + (y – 1) + 2(z – 1) = 0 hay 2x + y + 2z + 1 = 0.