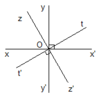
Cho bốn đường thẳng xx'. yy', zz', tt' cắt nhau tại O trong đó x O y ^ = 90 ° , z O t ^ = 90 ° . Trên hình vẽ có bao nhiêu góc?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 3 2017
Có 4 góc bẹt.
Có 8 góc vuông.
Có 8 góc nhọn.
Còn lại 28 − 4 + 8 + 8 = 8 (góc tù).
20 tháng 12 2019
+ Tổng số điểm phân biệt là: 4 + 5 + 6 + 7 + 1 = 23 điểm. Qua 2 điểm
vẽ được 1 đường thẳng nên ta có 23. 22 : 2 = 253 đường thẳng.
0,25
+ Mặt khác số các điểm thẳng hàng là 5;6;7;8 nên số các đường thẳng
trùng nhau là 10,15,21,28. Số đường thẳng cần tìm là: 253 - 10 - 15 -
0,25
21 - 28 + 4 = 183 đường thẳng
6 tháng 1 2020
Trên 4 đường thẳng xx' ; yy' ; zz' và tt' có số điểm phân biệt tương ứng là 5, 6, 7, 8 => Số tia lần lượt tương ứng là 10, 12, 14, 16 => Tổng số tia cần tìm là 10 + 12 + 14 + 16 = 52 tia.
Tổng số điểm phân biệt là : 4 + 5 + 6 + 7 + 1 = 23 điểm. Qua 2 điểm ta vẽ được 1 đường thẳng nên ta có 23 . 22 : 2 = 253 đường thẳng.
Mặt khác số các điểm thẳng hàng là 5, 6, 7, 8 nên số các đường thẳng trùng nhau là 10, 15, 21, 28. Số đường thẳng cần tìm là : 253 - 10 - 15 - 21 - 28 + 4 = 183 đường thẳng.
CM
12 tháng 12 2017
Trong đó có 3 góc bẹt x O x ' , y O y ' , z O z '
Có 4 góc vuông x O y , y O x ' , x ' O y ' , y ' O x
Có 4 góc nhọn x O z , z O y , x ' O z ' , z ' O y '
Có 4 góc tù x O z ' , x ' O z , y O z ' , z O y ' .
YN
26 tháng 6 2021
\(a)\)
\(zz'\) và \(tt'\)cắt nhau tại \(O\)và có một góc vuông
=> Các góc còn lại đều vuông
\(\Rightarrow\widehat{tOz}=\widehat{zOt'}=\widehat{t'Oz'}=\widehat{tOz'}=90^o\)
\(b)\)
Có hai cặp góc nhọn đối đỉnh:
\(+)\)\(\widehat{xOt};\widehat{x'Ot'}\)
\(+)\)\(\widehat{xOz};\widehat{x'Oz'}\)
Có hai cặp góc tù đối đỉnh:
\(+)\)\(\widehat{xOt'};\widehat{x'Ot}\)
\(+)\)\(\widehat{x'Oz};\widehat{xOz'}\)
Có 8 tia chung gốc.
Có 8.7 2 = 28 (góc).