Một vật có khối lượng 3kg được treo như hình vẽ,thanh AB vuông góc với tường thẳng đứng, CB lệch góc 600 so với phương ngang. Tính lực căng của dây BC và áp lực của thanh AB lên tường khi hệ cân bằng. Lấy g = 10 m / s 2
K
Khách
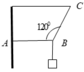
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
29 tháng 10 2018
Ta có P = mg = 3.10=30 (N)
Biểu diễn các lực như hình vẽ
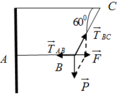
Theo điều kiện cân bằng
T → B C + T → A B + P → = 0 ⇒ F → + T → A B = 0
⇒ F → ↑ ↓ T → A B F = T A B
Ta có S i n 60 0 = P T B C
⇒ T B C = P S i n 60 0 = 30 3 2 = 20 3 ( N )
C o s 60 0 = F T B C = T A B T B C ⇒ T A B = C o s 60 0 . T B C = 1 2 .20. 3 = 10 3 ( N )
VT
17 tháng 12 2017
Chọn đáp án B
? Lời giải:
Cách 1: Biểu diễn các lực như hình vẽ:
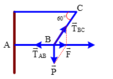
+ Theo điều kiện cân bằng:
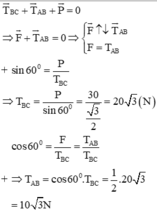
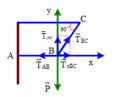
+ Chọn hệ quy chiếu Oxy như hình vẽ.
VT
16 tháng 12 2017
Biểu diễn các lực như hình vẽ
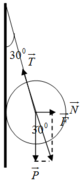
Theo điều kiện cân bằng
T → + N → + P → = 0 ⇒ F → + T → = 0
⇒ F → ↑ ↓ T → F = T
C o s 30 0 = P F ⇒ F = P C o s 30 0 = 30 3 2 = 20 3 ( N ) ⇒ T = 20 3 ( N )
S i n 30 0 = N F ⇒ N = F . S i n 30 0 = 20 3 . 1 2 = 10. 3 ( N )
VT
8 tháng 7 2019
Chọn đáp án B
? Lời giải:
Ta có P = mg = 3.10 = 30 (N)
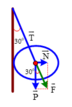
Cách 1: Biểu diễn các lực như hình vẽ
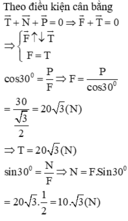
Cách 2:
Chọn hệ quy chiếu Oxy như hình vẽ.
VT
28 tháng 5 2017
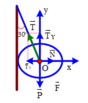
1. Ta có
P = m g = 6.10 = 60 ( k g ) S i n A C B ^ = A B B C = 30 60 ⇒ A C B ^ = 30 0 ⇒ A B C ^ = 60 0
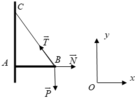
a, Phản lực N → có hướng A B → . Theo điều kiện cân bằng:
T → + P → + N → = 0 → ; T = P = 40 N
Chiếu lên Oy
T . cos 30 0 − P = 0 ⇒ T = P cos 30 0 = 60 3 2 = 40 3 ( N )
Chiếu lên Ox
⇒ T . sin 30 0 − N = 0 ⇒ N = 40 3 . 1 2 = 20 3 ( N )
b, Phản lực có phương nằm trong góc. Cân bằng đối với trục quay ở A:
M T → = M P → 1 + M P → 2 ⇒ T . A B sin 60 0 = P 1 . A B 2 + P 2 . A B ⇒ T = 3.10.0 , 5 + 60 3 2 = 50 3 ( N )
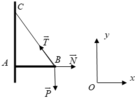
Phương trình cân bằng lực:
T → + P → 1 + P → 2 + N → = 0 →
Chiếu theo Ox
N x = T x = T cos 60 0 = 50. 3 2 = 25 3 ( N )
Chiếu theo Oy
N y + T y − P 1 − P 2 = 0 ⇒ N y = 30 + 60 − 50 3 . 3 2 = 15 ( N )
Vậy
N = N x 2 + N y 2 = 15 2 + ( 25 3 ) 2 = 10 21 ( N ) { N x = T x = T cos 60 0 = T 2 = 50 3 2 = 25 3 ( N ) N y = P + P ' − T ' cos α = ( m + m ' ) g − T ' cos α
2.Theo ý a ta có: T = m g cos A C B ^
Theo ý b ta có T = P 1 2 + P 2 cos A C B ^
Vậy khi tăng A C B ^ thì lực căng T tăng
VT
23 tháng 11 2018
Ta có P = mg = 3.10=30 (N)
Biểu diễn các lực như hình vẽ
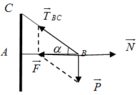
Theo điều kiện cân bằng
T → B C + N → + P → = 0 ⇒ F → + N → = 0
⇒ F → ↑ ↓ N → F = N
Xét tam giác ABC ta có
S i n α = A C B C = A C A B 2 + A C 2 = 30 30 2 + 40 2 = 3 5
C o s α = A B B C = A B A B 2 + A C 2 = 40 40 2 + 30 2 = 4 5
Theo hình biểu diễn
S i n α = P T B C ⇒ T B C = 30 3 5 = 50 ( N )
C o s α = F T B C = N T B C ⇒ N = T B C . C o s α = 50. 4 5 = 40 ( N )
VT
15 tháng 2 2017
Chọn A.
Các lực tác dụng lên thanh AB (tại B) như hình vẽ.
Điều kiện cân bằng:
P → + N → + T → = 0
Từ hệ thức lượng trong tam giác vuông thu được:
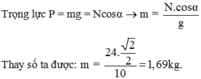
Vì α = 45° nên lực căng dây T = P = mg = 16,9N
Ta có P = mg = 3.10=30 (N)
Cách 1: Biểu diễn các lực như hình vẽ
T → B C + T → A B + P → = 0 ⇒ P → + T → = 0 ⇒ { P → ↑ ↓ T → P = T T a c ó : cos 30 0 = T T B C = P T B C ⇒ T B C = P cos 30 0 = 30 3 2 = 20 3 ( N ) sin 30 0 = T A B T B C ⇒ T A B = sin 30 0 . T B C = 1 2 .20. 3 = 10 3 ( N )
Cách 2: Chọn hệ quy chiếu Oxy như hình vẽ. Phân tích thành hai lực T → x B C , T → y B C như hình vẽ
Theo điều kiện cân bằng
T → B C + T → A B + P → = 0 ⇒ T → x B C + T → y B C + T → A B + P → = 0
Chiếu theo Ox:
T y B C − P = 0 ⇒ cos 30 0 . T B C = P ⇒ T B C = P cos 30 0 = 30 3 2 = 20 3 ( N )
Thay vào ( 1 ) ta có
T A B = 1 2 .20. 3 = 10. 3 ( N )