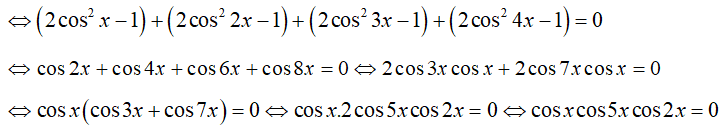giải bài 2x+22x+22x+24x=292
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
3 tháng 9 2021
1.
\(3sin^22x-2sin2x.cos2x-4cos^22x=2\)
\(\Leftrightarrow-\dfrac{3}{2}\left(1-2sin^22x\right)-2sin2x.cos2x-2\left(2cos^22x-1\right)=\dfrac{5}{2}\)
\(\Leftrightarrow sin4x+\dfrac{7}{2}cos4x=-\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{53}}{2}\left(\dfrac{2}{\sqrt{53}}sin4x+\dfrac{7}{\sqrt{53}}cos4x\right)=-\dfrac{5}{2}\)
\(\Leftrightarrow sin\left(4x+arccos\dfrac{2}{\sqrt{53}}\right)=-\dfrac{5}{\sqrt{53}}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+arccos\dfrac{2}{\sqrt{53}}=arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+k2\pi\\4x+arccos\dfrac{2}{\sqrt{53}}=\pi-arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{4}arccos\dfrac{2}{\sqrt{53}}+\dfrac{1}{4}arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arccos\dfrac{2}{\sqrt{53}}-\dfrac{1}{4}arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+\dfrac{k\pi}{2}\end{matrix}\right.\)
HP
3 tháng 9 2021
2.
\(2\sqrt{3}cos^2x+6sinx.cosx=3+\sqrt{3}\)
\(\Leftrightarrow\sqrt{3}\left(2cos^2x-1\right)+6sinx.cosx=3\)
\(\Leftrightarrow\sqrt{3}cos2x+3sin2x=3\)
\(\Leftrightarrow2\sqrt{3}\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)=3\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\pi\end{matrix}\right.\)
12 tháng 9 2016
a)\(pt\Leftrightarrow\frac{1-cos8x}{2}+\frac{1-cos6x}{2}=\frac{1-cos4x}{2}+\frac{1-cos2x}{2}\)
\(\Leftrightarrow cos2x+cos4x=cos6x+cos8x\)
\(\Leftrightarrow2cos3x\cdot cosx=2cos7x\cdot cosx\)
\(\Leftrightarrow2cos\left(cos3x-cos7x\right)=0\)
\(\Leftrightarrow2cosx\cdot\left(-2\right)\cdot sin5x\cdot sin\left(-2x\right)=0\)
\(\Leftrightarrow cosx\cdot sin2x\cdot sin5x=0\)
\(\Leftrightarrow sin2x\cdot sin5x=0\)(do sin2x=0 <=>2sinx*cosx=0 gồm th cosx=0 r`)
\(\Leftrightarrow\left[\begin{array}{nghiempt}sin2x=0\\sin5x=0\end{array}\right.\)\(\Rightarrow\left[\begin{array}{nghiempt}x=\frac{k\pi}{2}\\x=\frac{k\pi}{5}\end{array}\right.\)\(\left(k\in Z\right)\)
12 tháng 9 2016
b)\(pt\Leftrightarrow1-cos2x+1-cos4x=1+cos6x+1+cos8x\)
\(\Leftrightarrow cos2x+cos8x+cos4x+cos6x=0\)
\(\Leftrightarrow cos10x\cdot cos6x+cos10x\cdot cos2x=0\)
\(\Leftrightarrow cos10x\left(cos6x+cos2x\right)=0\)
\(\Leftrightarrow cos10x\cdot cos8x\cdot cos4x=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}cos10x=0\\cos8x=0\\cos4x=0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=\frac{\pi}{20}+\frac{k\pi}{10}\\x=\frac{\pi}{16}+\frac{k\pi}{8}\\x=\frac{\pi}{8}+\frac{k\pi}{4}\end{array}\right.\)
TN
0
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2020
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos6x=\frac{1}{2}+\frac{1}{2}cos4x+\frac{1}{2}+\frac{1}{2}cos8x\)
\(\Leftrightarrow cos8x+cos2x+cos6x+cos4x=0\)
\(\Leftrightarrow2cos5x.cos3x+2cos5x.cosx=0\)
\(\Leftrightarrow cos5x\left(cos3x+cosx\right)=0\)
\(\Leftrightarrow2cos5x.cos2x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=0\\cos2x=0\\cosx=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{10}+\frac{k\pi}{5}\\x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\frac{\pi}{2}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2020
\(\Leftrightarrow2cos^2x-1+2cos^22x-1+2cos^23x-1+2cos^24x=0\)
\(\Leftrightarrow cos2x+cos4x+cos6x+2cos^24x=0\)
\(\Leftrightarrow2cos4x.cos2x+cos4x+2cos^24x=0\)
\(\Leftrightarrow cos4x\left(2cos2x+1+2cos4x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\2cos4x+2cos2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2\left(2cos^22x-1\right)+2cos2x+1=0\)
\(\Leftrightarrow4cos^22x+2cos2x-1=0\)
\(\Rightarrow\left[{}\begin{matrix}cos2x=\frac{\sqrt{5}-1}{4}=cos\left(\frac{2\pi}{5}\right)\\cos2x=\frac{-\sqrt{5}-1}{4}=cos\left(\frac{4\pi}{5}\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
\(2-2cos^22x=cos2x+1\)
\(\Leftrightarrow2cos^22x+cos2x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)