Sắp xếp các số thực: - 3 , 2 ; 1 ; - 1 2 ; 7 , 4 ; 0 ; - 1 , 5 . Theo thứ tự từ nhỏ đến lớn các giá trị tuyệt đối của chúng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
9 tháng 11 2023
1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.
2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
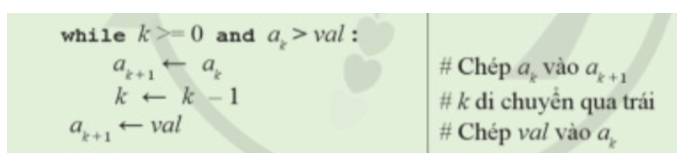
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Ta có:
\(-\frac{2}{3} = -0,\left( 6 \right);\,\,\,\,\,4,1;\,\,\, - \sqrt 2 = - 1,414...;\,\,\,\,3,2;\\\pi = 3,141...;\,\,\,\, - \frac{3}{4} = - 0,75;\,\,\,\,\frac{7}{3} = 2,\left( 3 \right)\).
Do \( - 1,414... < - 0,75 < -0,\left( 6 \right) < 2,\left( 3 \right) < 3,141... < 3,2 < 4,1\)
Nên \( - \sqrt 2 < - \frac{3}{4} < -\frac{2}{3} < \frac{7}{3} < \pi < 3,2 < 4,1.\)
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
Ta có:
\(\frac{{ - 2}}{5} = \frac{{ - 2.8}}{{5.8}} = \frac{{ - 16}}{{40}}\)
\(\frac{{ - 3}}{8} = \frac{{ - 3.5}}{{8.5}} = \frac{{ - 15}}{{40}}\)
\(\frac{3}{{ - 4}} = \frac{{ - 3}}{4} = \frac{{ - 3.10}}{{4.10}} = \frac{{ - 30}}{{40}}\)
Do -30 < -16 < -15 nên \(\frac{{ - 30}}{{40}} < \frac{{ - 16}}{{40}} < \frac{{ - 15}}{{40}}\). Do đó \(\frac{3}{{ - 4}} < \frac{{ - 2}}{5} < \frac{{ - 3}}{8}\).
QT
Quoc Tran Anh Le
Giáo viên
13 tháng 9 2023
- Sắp xếp theo thứ tự tăng dần của cột Tốt
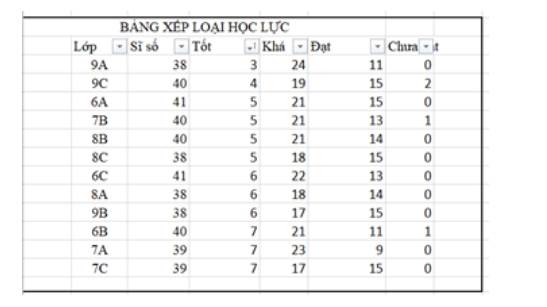
- Sắp xếp theo thứ tự giảm dần của cột Sĩ số
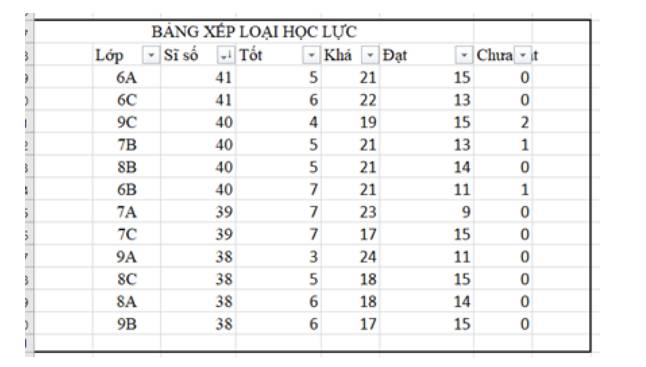
- Kết quả bảng dữ liệu được sắp xếp theo thứ tự trên một cột chính, nếu có nhiều dòng có giá trị khác nhau trên cột chính thì chúng sẽ được sắp xếp theo thứ tự trên cột phụ (khác với cột chính). Ví dụ, trong hoạt động trên, cột Sĩ số được coi là cột chính, cột Tốt là cột phụ. Do đó, cách sắp xếp số lượng học sinh xếp loại tốt của các lớp có cùng sĩ số theo thứ tự tăng dần của cột tốt.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
*Thuật toán sắp xếp chèn (Insertion Sort):
import time
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp chèn
insertion_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là 0 giây
*Thuật toán sắp xếp chọn:
import time
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp chọn
selection_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là: 0 giây
*Thuật toán sắp xếp nổi bọt:
import time
def bubble_sort(arr):
n = len(arr)
for i in range(n - 1):
for j in range(n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp nổi bọt
bubble_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là: 0 giây
PT
1
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
# Nhập dãy số từ bàn phím
lst = list(map(int, input("Nhập dãy số cách nhau bởi dấu cách: ").split()))
# Sắp xếp dãy số theo thuật toán sắp xếp chọn
for i in range(len(lst)):
min_idx = i
for j in range(i+1, len(lst)):
if lst[j] < lst[min_idx]:
min_idx = j
lst[i], lst[min_idx] = lst[min_idx], lst[i]
# In kết quả ra màn hình
print("Dãy số đã sắp xếp:", lst)
NN
1
1 tháng 1 2022
#include <bits/stdc++.h>
using namespace std;
long long i,n,t,x;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x>0) t=t+x;
}
cout<<t;
return 0;
}
ML
1
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
- Bước 1: i = 0;
- Bước 2: Tìm phần tử a[min] nhỏ nhất trong dãy hiện hành từ a[i] đến a[n-1].
- Bước 3: Đổi chỗ a[min] và a[i].
- Bước 4: Nếu i < n-1 thì gán i = i+1; rồi lặp lại bước 2, ngược lại -> Dừng.
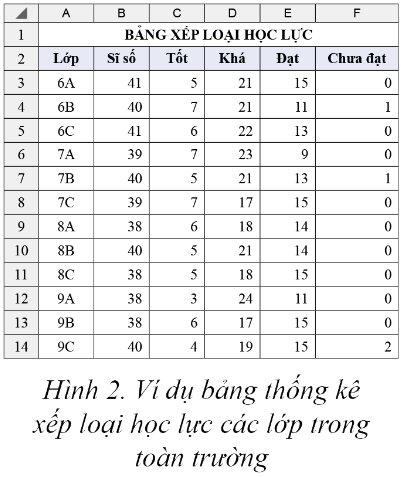
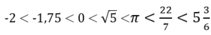
Ta có