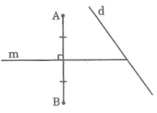
Cho đường thẳng d và hai điểm A, B thuộc cùng một nửa mặt phẳng có bờ d. Tìm một điểm C nằm trên d sao cho C cách đều A và B.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

các đoạn thẳng nối hai trong bốn điểm A, B, C, D thì đường thẳng a cắt AC, AD, BC, BD và không cắt AB, CD
Trong các đoạn thẳng nối hai trong bốn điểm A, B, C, D thì đường thẳng a cắt AC, AD, BC, BD và không cắt AB, CD.

Đáp án là B
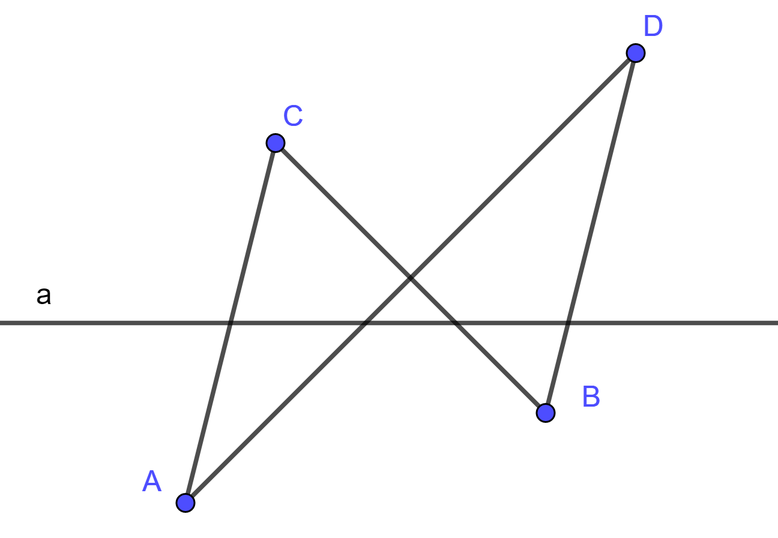
Vì A và B thuộc cùng một nửa mặt phẳng bờ a, còn C và D thuộc nửa mặt phẳng kia nên:
A và C nằm ở hai nửa mặt phẳng đối nhau bờ là đường thẳng a nên a cắt đoạn AC
A và D nằm ở hai nửa mặt phẳng đối nhau bờ là đường thẳng a nên a cắt đoạn AD
B và C nằm ở hai nửa mặt phẳng đối nhau bờ là đường thẳng a nên a cắt đoạn BC
B và D nằm ở hai nửa mặt phẳng đối nhau bờ là đường thẳng a nên a cắt đoạn BD
Vậy đường thẳng a cắt 4 đoạn thẳng

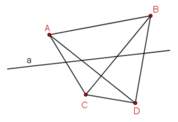
Điểm A, B cùng nằm trên một mặt phẳng bờ a , điểm C, D cùng nằm trên một nửa mặt phẳng đường thẳng a không cắt đoạn thẳng AB cũng không cắt đoạn thẳng CD. Trong khi đó đường thẳng a cắt đoạn thẳng AC, AD, BC, BD.

A, B năm trên cùng một mắt phẳng với a và cùng nằm một nửa mặt phẳng bờ a => a không cắt AB
Tương tự như vậy a cũng không cắt CD
A, C nằm trên cùng mặt phẳng với a nhưng mỗi điểm ở mỗi bờ mặt phẳng khác nhau nên a cắt AC
Tương tự như vậy a cũng cắt BD
* Nếu AB không vuông góc với d
- Vì điểm C cách đều hai điểm A và B nên C nằm trên đường trung trực của AB.
- Điểm C ∈ d
Vậy C là giao điểm của đường trung trực của AB và đường thẳng d.
Cần dựng đường thẳng m là đường trung trực của đoạn thẳng AB cắt đường thẳng d tại C.
Vậy C là điểm cần tìm.
* Nếu AB vuông góc với d
Khi đó đường trung trực của AB song song với đường thẳng d nên không tồn tại điểm C.