Tìm x, y biết x 2 + y 2 10 = x 2 - 2 y 2 7 và x4.y4 = 81.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ phương trình đầu ta rút ra được: x^2 = 9y^2 => x = 3y hay x = -3y
Từ phương trình 2 ta được: x^2*y^2 = 9 => xy = 3 hay xy = -3
Vậy ta được các hệ phương trình sau:
x=3y và xy = 3 => (x,y) = (3,1) và (x,y) = (-3,-1)
x=3y và xy = -3 => loại (bạn có thể biện luận x = 3y thì x, y cùng dấy loại ngay hệ này)
x= - 3y và xy = 3 => loại (bạn có thể biện luận x = -3y thì x, y khác dấy nhưng pt2 lại phải cùng dấy loại ngay hệ này)
x= - 3y và xy = - 3 => (x,y) = (3,-1) và (x,y) = (-3,1)
Vậy hệ có 4 cặp nghiệm

Ta có:
\(\frac{x}{2}=\frac{y}{-5}=\frac{x-y}{2-\left(-5\right)}=\frac{-7}{7}=-1\)
\(\Rightarrow x=-1.2=-2\)
\(\Rightarrow y=-1.\left(-5\right)=5\)
x:2=y:(-5) và x-y=(-7)
x:2=y:(-5) suy ra x/2=y/(-5)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/2=y/(-5)=x-y/2-(-5)=-7/7=(-1)
x/2=(-1) suy ra x=(-1)*2=(-2)
y/(-5)=(-1) suy ra y=(-1)*(-5)=5
vậy x=(-2) và y=5

Bài 3:
\(\Leftrightarrow3^{2x+6}=3\)
=>2x+6=1
=>2x=-5
hay x=-5/2

Đặt \(\begin{cases}x^2=a\left(a\ge0\right)\\y^2=b\left(b\ge0\right)\end{cases}\), khi đó ta có:
\(\frac{a+b}{10}=\frac{a-2b}{7}\) và \(a^2b^2=81\). Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{a+b}{10}=\frac{a-2b}{7}=\frac{\left(a+b\right)-\left(a-2b\right)}{10-7}=\frac{3b}{3}=b\left(1\right)\)
\(\frac{a+b}{10}=\frac{a-2b}{7}=\frac{2a+2b}{20}=\frac{\left(2a+2b\right)+\left(a-2b\right)}{20+7}=\frac{3a}{27}=\frac{a}{9}\left(2\right)\)
Từ (1) và (2) suy ra \(\frac{a}{9}=b\Rightarrow a=9b\) thay vào \(a^2b^2=81\) ta có:
\(\left(9b\right)^2\cdot b^2=81\Rightarrow81\cdot b^4=81\Rightarrow b^4=1\Rightarrow b=1\) (b\(\ge\)0)
Suy ra \(a=9b=9\cdot1=9\)
\(\Rightarrow\begin{cases}x^2=9\\y^2=1\end{cases}\)\(\Rightarrow\begin{cases}x=\pm3\\y=\pm1\end{cases}\)

Ta co x/2 = y/5 =>x=(2y)/5 (1)
Lai co xy =10 (2)
Thay (1) vao (2) ta duoc (2y)/5.y=10=>(2y2)/5=10=>y2=10.(5/2)=>y2=25=>y=5 va y=-5
Khi y=5 thi x =10:5=2
Khi y=-5 thi x = 10 : (-5)=-2 quên tìm x h bổ sung :) -...-


#)Giải :
a) Đặt \(\frac{x}{3}=\frac{y}{7}=k\Rightarrow\hept{\begin{cases}x=3k\\y=7k\end{cases}}\)
\(\Rightarrow3k.7k=84\Rightarrow21k^2=84\Rightarrow k^2=4\Rightarrow\orbr{\begin{cases}k=2\\k=-2\end{cases}}\)
Nếu k = 2 \(\Rightarrow\hept{\begin{cases}\frac{x}{3}=2\\\frac{y}{7}=2\end{cases}\Rightarrow\hept{\begin{cases}x=6\\y=14\end{cases}}}\)
Nếu k = -2 \(\Rightarrow\hept{\begin{cases}\frac{x}{3}=-2\\\frac{y}{7}=-2\end{cases}\Rightarrow\hept{\begin{cases}x=-6\\y=-14\end{cases}}}\)
Vậy ...
Đặt x2 = a (a ≥ 0), y2 = b (b ≥ 0)
Ta có: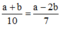 và a2b2 = 81.
và a2b2 = 81.
Theo tính chất của dãy tỉ số bằng nhau ta có:
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b
Do a2b2 = 81 nên (9b)2.b2 = 81 ⇒ 81b4 = 81 ⇒ b4 = 1 ⇒ b = 1 (vì b ≥ 0)
Suy ra a = 9. 1 = 9
Ta có x2 = 9 và y2 = 1. Suy ra x = 3 hoặc x = -3, y = 1 hoặc y = -1.