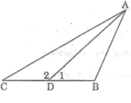
Cho tam giác ABC có B > 90o, điểm D nằm giữa B và C. Chứng minh rằng AB < AD < AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
0
18 tháng 3 2016
A B C D
góc B > 90 độ
\(\Rightarrow\)cạnh huyền AD lớn nhất => AB < AD (1)
góc ADC > góc B = 90 độ (góc ngoài tại D của tam giác ABD)
=> góc ADC > 90 độ => cạnh huyền AC lớn nhất => AD < AC (2)
Từ (1) và (2), => AB < AD <AC (đpcm)
SG
1
18 tháng 5 2022
Xét ΔABD có \(\widehat{B}>90^0\)
nen AD là cạnh lớn nhất
=>AB<AD(1)
XétΔADC có \(\widehat{ADC}>90^0\)
nên AC là cạnh lớn nhất
=>AD<AC(2)
Từ (1) và (2) suy ra AB<AD<AC
DG
0
MA
1
HT
17 tháng 2 2016
trong tam giác ABD có góc B > 90 độ => góc B là góc lớn nhất và góc ADB <90 độ
=> AD> AB ( quan hệ góc cạnh trong tam giác) hay AB<AD (1)
có góc ADB + góc ADC = 180 độ mà góc ADB < 90 độ
=> góc ADC > 90 độ
trong tam giác ADC có góc ADC > góc ACD => AC> AD hay AD<AC (2)
từ (1) và (2) => AB< AD< AC
MA
0
29 tháng 4 2017
B C A D
Xét tam giác ABD có góc ABD>90o =>góc ABD là góc lớn nhất trong tam giác=>cạnh AD là cạnh lớn nhất=>AD>AB(1)
Xét tam giác ADC có góc ADC=góc ABD + góc BAD
Do ABD>900=>góc ADC>900
=>góc ADC là góc lớn nhất trong tam giác ADC=>cạnh AC là cạnh lớn nhất trong tam giác ADC=>AC>AD(2)
Từ (1) và (2)=> AB<AD<AC
Trong ∆ABD ta có: ∠B > 90o
⇒ ∠B > ∠D1 ( trong 1 tam giác, góc tù là góc lớn nhất- chú ý tổng ba góc trong một tam giác bằng 180º) ⇒ AD > AB (đối diện góc lớn hơn là cạnh lớn hơn) (1)
Trong ΔABD ta có: ∠D2 là góc ngoài tại đỉnh D nên ∠D2 = ∠B + ∠BAD. Suy ra: ∠D2 > ∠B > 90o
Trong ΔADC ta có: ∠D2 > 90o
⇒ ∠D2 > ∠C ⇒ AC > AD (cạnh đối diện góc lớn hơn là cạnh lớn hơn) (2)
Từ (1) và (2) suy ra: AB < AD < AC