Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA. Hãy so sánh các góc AMB và ANC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2018
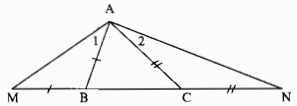
Trong ∆ABC có AB < AC
⇒ góc ABC= góc ACB (đối diện cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt)
⇒ góc ∆ABM cân tại B
⇒ góc M = góc A1(tính chất tam giác cân)
Trong ∆ABM ta có có góc ngoài tại đỉnh B
góc ABC= góc M+ góc A1
Suy ra: góc M=12 góc ABC (2)
Ta có: AC = CN (gt)
⇒ ∆CAN cân tại C⇒ góc N= góc A2 (tính chất tam giác cân)
Trong ∆CAN ta có góc ACB là góc ngoài tại đỉnh C.
⇒góc ACB= góc N+ góc A2
Suy ra: góc N=12 góc ACB (3)
Từ (1), (2) và (3) suy ra: góc M > góc N
b) Trong ∆AMN ta có: góc M> góc N
CM
29 tháng 7 2018
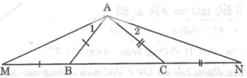
Trong ΔAMN, ta có: ∠(AMB) > ∠(ANC)
Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).
3 tháng 5 2015
Theo đề bài ta vẽ được hình trên, và dễ dàng nhận thấy tam giác OBC là tam giác cân tại đỉnh O.
Giải thích:
* Xét tam giác CKN vuông tại K và tam giác BHM vuông tại H, ta có:
CN=BM (đề bài cho)
nên ta chứng minh được hai tam giác vuông CKN và BHM bằng nhau (Trường hợp hai tam giác vuông có cạnh huyền bằng nhau).
Vậy cặp góc tương ứng MBH và góc NCK bằng nhau.
Mà góc NCK= góc BCO (đối dỉnh) (1)
Và góc MBH = góc CBO (đối đỉnh) (2)
Từ (1)(2) ta chứng minh được góc BCO = góc CBO .
vậy tam giác OBC cân tại O.
12 tháng 1
a: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
b:
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
c: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}\) nhọn
=>\(\widehat{ABM}=180^0-\widehat{ABC}>90^0\)
Xét ΔABM có \(\widehat{ABM}>90^0\)
mà AM là cạnh đối diện của góc ABM
nên AM là cạnh lớn nhất trong ΔABM
=>AM>AB
mà AB=AC
nên AM>AC
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .