Vẽ tam giác ABC biết ∠B =90o,∠C =60o, BC = 2cm. Sau đó đo AC để kiểm tra rằng AC = 4cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình vẽ:
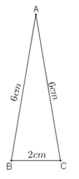
-) Dùng thước dựng đoạn thẳng BC = 2 cm.
-) Dùng compa dựng cung tròn tâm B, bán kính R = 6cm và dựng cung tròn tâm C, bán kính R = 6cm.
Hai cung tròn này cắt nhau tại A. Nối B với A, C với A.
Ta được tam giác ABC thỏa mãn đầu bài.
-) Dùng thước đo độ ta được: ∠A ≈ 20º

B A C 2cm 60
Ta có : \(\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180^o\)
\(\Leftrightarrow\widehat{BAC}+90^o+60^o=180^o\)
\(\Leftrightarrow\widehat{BAC}=30^o\)
Xét \(\Delta ABC\)vuông tại B có \(\widehat{BAC}=30^o\)
\(\Rightarrow BC=\frac{1}{2}AC\Leftrightarrow AC=2BC\)
\(\Leftrightarrow AC=2.2=4\left(cm\right)\)
( * ghi nhớ : trong tam giác vuông cạnh đối diện vs góc 30 độ bằng nửa cạnh huyền )
Vậy ...

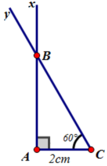
Cách vẽ:
- Vẽ đoạn thẳng AC = 2cm
- Trên cùng một nửa mặt phẳng bờ AC vẽ các tia Ax và Cy sao cho 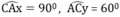
Hai tia cắt nhau tại B. Ta được tam giác ABC cần vẽ.

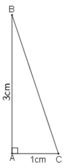
- Vẽ góc ∠ xAy = 90º
- Trên tia Ax lấy điểm B sao cho AB = 3cm.
Trên tia Ay lấy điểm C sao cho AC = 1cm.
- Nối các điểm B và C ta được tam giác ABC thỏa mãn.
Đo góc C ta được ∠C ≈ 72o.
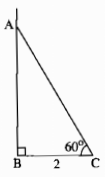

+ Vẽ tam giác ABC:
-) Vẽ đoạn thẳng BC = 2 cm.
-) Trên cùng một nửa mặt phăng bờ BC, vẽ các tia Bx và Cy sao cho ∠CBx = 90º và &BCy = 60º.
Hai tia trên cắt nhau tại A ta được tam giác ABC.
+) Đo AC ta được: AC = 4cm.