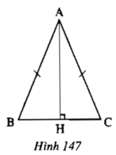
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (hình 147). Chứng minh rằng ΔAHB =ΔAHC (giải bằng 2 cách)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Xét tam giác vuông AHB và tam giác vuông AHC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AHB = tam giác vuông AHC ( cạnh huyền. góc nhọn)
=> HB = HC ( 2 cạnh tương ứng )
b.Xét tam giác vuông ADH và tam giác vuông AEH, có:
AH: cạnh chung
góc DAH = góc EAH ( AH là đường cao cũng là đường phân giác )
Vậy tam giác vuông ADH = tam giác vuông AEH
=> HD = HE ( 2 cạnh tương ứng )
=> tam giác HDE cân tại H
c.Xét tam giác vuông AEC và tam giác vuông ADB, có:
AB = AC ( ABC cân )
góc A: chung
Vậy tam giác vuông AEC = tam giác vuông ADB ( cạnh huyền.góc nhọn)
=> AD = AE ( 2 cạnh tương ứng )
=> tam giác ADE cân tại A
=> AH vuông với DE, mà AH cũng vuông với BC
=> DE//BC ( DE ko phải DC nha bạn )
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó:ΔAHB=ΔAHC
Suy ra: HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
c: Ta có: ΔADH=ΔAEH
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC

a/ Xét tam giác AHB và tam giác AHC
Góc AHB=AHC=90 độ
AB=AC(tam giác ABC cân tại A)
Góc B=C (tam giác ABC cân tại A)
=> Tam giác ABH=ACH(ch-gn)
mk nha

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔABH=ΔACH
nên HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHKB=ΔHIC

Lời giải:
a) Xét tam giác $AHB$ và $AHC$ có:
$AH$ chung
$AB=AC$ do $ABC$ cân tại $A$
$\widehat{AHB}=\widehat{AHC}=90^0$
$\Rightarrow \triangle AHB=\triangle AHC$ (ch-cgv)
b)
Vì $ABC$ cân tại $A$ nên $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABD}=\widehat{ACE}$
Xét tam giác $ABD$ và $ACE$ có:
$BD=CE$
$AB=AC$
$\widehat{ABD}=\widehat{ACE}$ (cmt)
$\Rightarrow \triangle ABD=\triangle ACE$ (c.g.c)
$\Rightarrow AD=AE$ nên $ADE$ là tam giác cân.

a: Xét ΔAHB và ΔAHC có
AH chung
AB=AC
HB=HC
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao

theo dề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2
theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )

theo đề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2 theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )

a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :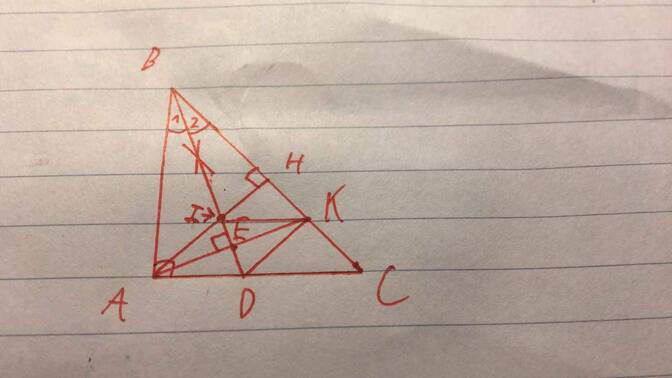
- Cách 1: ΔABC cân tại A nên ∠B = ∠C và AB = AC
Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:
AB = AC (GT)
∠B = ∠C
⇒ ΔAHB =ΔAHC (cạnh huyền – góc nhọn)
- Cách 2:
Xét hai tam giác vuông ΔAHB và ΔAHC đều vuông tại H có:
AB = AC
AH chung
⇒ ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)