Cho hàm số y = 2x
Biểu diễn các cặp số đó trên mặt phẳng tọa độ Oxy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

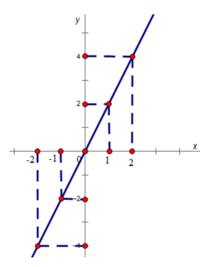

a)
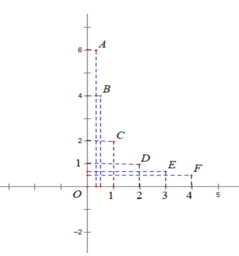
b)Bảng giá trị
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua 2 điểm (0; 0) và (1; 2)
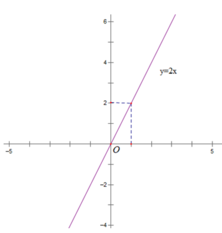

a) Ta có đồ thị hàm số \(y = - 2{x^2}\)
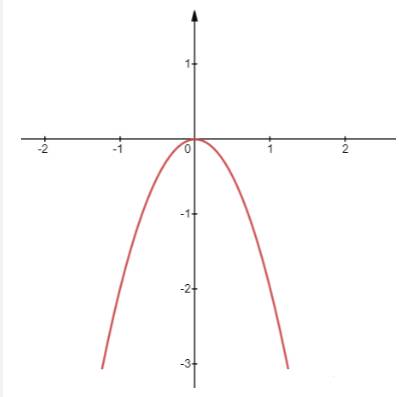
Nhìn vào 2 đồ thị, ta thấy dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\)giống với dạng đồ thị \(y = - 2{x^2}\)
b) Tọa độ điểm cao nhất là \(\left( {5;50} \right)\)
c) Ta có: \(S(x) = y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\)
\({(x - 5)^2} \ge 0 \Rightarrow - 2{(x - 5)^2} + 50 \le 50 \Rightarrow S(x) \le 50\)
Do đó diện tích lớn nhất của mảnh đất rào chắn là 50 \(({m^2})\) khi x = 5.