Trên cung nhỏ A B ⏜ của (O), cho hai điểm C và D sao cho cung A B ⏜ được chia thành ba cung bằng nhau ( A C ⏜ = C D ⏜ = D B ⏜ ). Bán kính OC và OD cắt dây AB lần lượt tại E và F
a, Hãy so sánh các đoạn thẳng AE và FB
b, Chứng minh các đường thẳng AB và CD song song


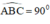
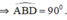
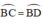 ( định lý )
( định lý )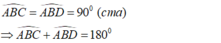
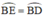 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 
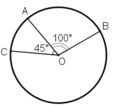

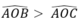 nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.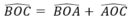 = 100
= 100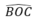 )
)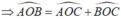
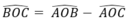 = 100
= 100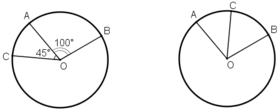
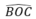
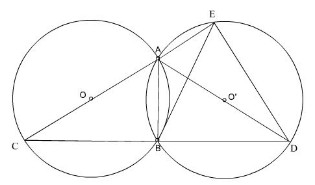
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD