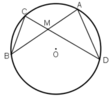
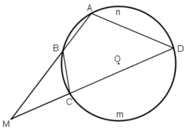
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.
Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.

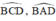 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 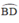
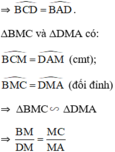
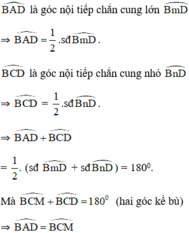
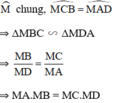



TH1: M nằm trong đường tròn.
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
ΔMBC và ΔMDA có:
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.