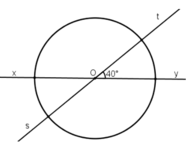
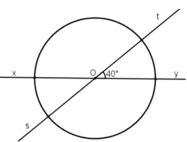
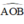Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40 ° . Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 5 2018
Đúng(0)
Những câu hỏi liên quan
LH
7 tháng 4 2017
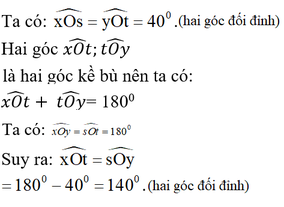
Ta có :
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)
14 tháng 1
a: Xét tứ giác BEFC có \(\widehat{BEC}=\widehat{BFC}=90^0\)
nên BEFC là tứ giác nội tiếp đường tròn đường kính BC
=>B,E,F,C cùng thuộc một đường tròn
tâm I là trung điểm của BC
b: Xét ΔABC có
BF,CE là các đường cao
BF cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
=>AM\(\perp\)BC
Xét (O) có
ΔAMD nội tiếp
AD là đường kính
Do đó: ΔAMD vuông tại M
=>AM\(\perp\)MD
Ta có: AM\(\perp\)BC
AM\(\perp\)MD
Do đó: BC//MD
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Ta có: \(\widehat{BAH}+\widehat{ABC}=90^0\)(AH\(\perp\)BC)
\(\widehat{ADC}+\widehat{CAD}=90^0\)(ΔACD vuông tại C)
mà \(\widehat{ABC}=\widehat{ADC}\)
nên \(\widehat{BAH}=\widehat{CAD}\)
=>\(\widehat{BAH}+\widehat{MAD}=\widehat{CAD}+\widehat{MAD}\)
=>\(\widehat{BAD}=\widehat{CAM}\)(1)
Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn cung BD
\(\widehat{BCD}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{BAD}=\widehat{BCD}\left(2\right)\)
Xét (O) có
\(\widehat{CBM}\) là góc nội tiếp chắn cung CM
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
Do đó: \(\widehat{CBM}=\widehat{CAM}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{CBM}=\widehat{BCD}\)
Xét tứ giác BCDM có BC//DM
nên BCDM là hình thang
Hình thang BCDM có \(\widehat{CBM}=\widehat{BCD}\)
nên BCDM là hình thang cân
c: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BA\(\perp\)BD
mà CH\(\perp\)BA
nên CH//BD
Ta có: CD\(\perp\)CA
BH\(\perp\)AC
Do đó: BH//CD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà I là trung điểm của BC
nên I là trung điểm của HD
=>H,I,D thẳng hàng
d: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AFE}\left(=180^0-\widehat{EFC}\right)\)
nên \(\widehat{xAC}=\widehat{AFE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EF//Ax
Ta có: Ax//EF
Ax\(\perp\)AD
Do đó: AD\(\perp\)EF tại K
bằng 110º. Tính ba góc còn lại
– 
, 
, 
.
< 
)
, 