Dựng tam giác ABC, biết BC = 6cm, góc A = 40o và đường cao AH = 4cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


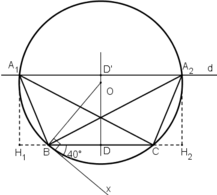
Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40 º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 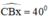
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40 º dựng trên đoạn BC
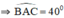
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=1\cdot4=4\)
=>\(AH=\sqrt{4}=2\left(cm\right)\)
BC=BH+CH
=>BC=1+4=5(cm)
XétΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB^2=1\cdot5=5\\AC^2=4\cdot5=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{\sqrt{5}}{5}\)
nên \(\widehat{C}\simeq27^0\)
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-27^0=63^0\)
b: AH=2cm
=>H thuộc (A;2cm)
Xét (A;2cm) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A;2cm)
c: Sửa đề: BDEH
Xét ΔAHB vuông tại H và ΔADE vuông tại D có
AH=AD
\(\widehat{HAB}=\widehat{DAE}\)
Do đó: ΔAHB=ΔADE
=>HB=DE
Xét tứ giác BDEH có
BH//ED
BH=ED
Do đó: BDEH là hình bình hành

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

\(\sin\widehat{C}=\dfrac{AB}{BC}=\sin35^0\approx0,6\Leftrightarrow AB=0,6\cdot6=3,6\left(cm\right)\\ \Leftrightarrow AC=\sqrt{BC^2-AB^2}=4,8\left(cm\right)\)


Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán

Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC

+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.
Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho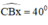
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.