Cho cấp số cộng: u1; u2; u3;… có công sai d.Biết u4 + u8 + u12 + u16 = 224. Tính S19.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2019
Chọn A
Ta có:
u 4 = u 1 + 3 d u 14 = u 1 + 13 d
Suy ra chọn đáp án A.
CM
3 tháng 12 2019
Số hạng tổng quát của cấp số cộng ( u n ) là:
u n = u 1 + n − 1 .0 , 1 ⇒ u 7 = − 0 , 1 + 7 − 1 .0 , 1 = 0 , 5
Chọn đáp án C.
CM
10 tháng 1 2018
Chọn C
Số hạng tổng quát của cấp số cộng (un) là:
u n = u 1 + n − 1 .0,1 ⇒ u 7 = − 0,1 + 7 − 1 .0,1 = 0,5
CM
17 tháng 7 2019
Đáp án A
Ta có
u 1 − u 3 = 6 u 5 = − 10 ⇔ u 1 − u 1 + 2 d = 6 u 1 + 4 d = − 10 ⇔ − 2 d = 6 u 1 = − 10 − 4 d ⇔ d = − 3 u 1 = 2 .
Vậy
u n = u 1 + n − 1 d = 2 − 3 n − 1 = 5 − 3 n .
CM
7 tháng 11 2018
u 1 = − 5 d = 3 → n ↔ u n = 100 100 = u n = u 1 + n − 1 d = − 5 + ( n − 1 ) .3 ⇔ 100 = 3 n − 8 ⇔ 3 n = 108 ⇔ n = 36
Chọn đáp án D
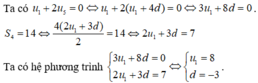
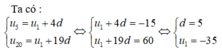
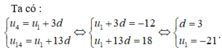
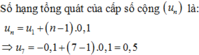
Chọn C.
Có: u4 + u8 + u12 + u16 = 224 ⇔ u1 + 3d + u1 + 7d + u1 + 15d = 224
⇔ 4 u1 + 36d = 224 ⇔ u1 + 9d = 56
Ta có: S19 = 19/2. (2 u1 + 18d) = 19(u1 + 9d) = 19.56 = 1064