Cho CSN (un) thỏa: u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11 Tìm công bội và số hạng tổng quát của cấp số
A. q = 3 ; u n = 3 n - 1 11
B. q = 1 3 ; u n = 81 11 . 1 3 n - 1
C. Cả A, B đúng
D. Cả A, B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u_3+u_7+...+u_{35}=u_1q^2+u_1q^6+...+u_1q^{34}\)
\(=u_1q^2\left(1+q^4+q^8+...+q^{32}\right)=u_1q^2.\frac{\left(q^4\right)^9-1}{q^4-1}=524286\)
2/ \(u_1^2+u_2^2+...+u_{20}^2=u_1^2+u_1^2q^2+u_1^2q^4+...+u_1^2q^{38}\)
\(=u_1^2\left(1+q^2+q^4+...+q^{38}\right)=u_1^2\frac{\left(q^2\right)^{20}-1}{q^2-1}=\frac{3^{20}-1}{2}\)
3/
\(u_1=2;u_n=18\)
\(u_1^2+u_2^2+...+u_n^2=484\)
\(\Leftrightarrow u_1^2+u_1^2q^2+...+u_1^2q^{2\left(n-1\right)}=484\)
\(\Leftrightarrow u_1^2\left(1+q^2+...+q^{2\left(n-1\right)}\right)=484\)
\(\Leftrightarrow1+q^2+...+q^{2\left(n-1\right)}=121\)
\(\Leftrightarrow\frac{q^{2n}-1}{q^2-1}=121\)
Mà \(u_n=u_1q^{n-1}\Rightarrow q^{n-1}=\frac{u_n}{u_1}=9\Rightarrow q^n=9q\Rightarrow q^{2n}=81q^2\)
\(\Rightarrow\frac{81q^2-1}{q^2-1}=121\Rightarrow81q^2-1=121q^2-121\)
\(\Rightarrow q^2=3\Rightarrow q=\pm\sqrt{3}\)

Xét hàm số \(f\left(x\right)=\dfrac{x^{2022}+3x+16}{x^{2021}-x+11}\), ta cần cm
\(f\left(x\right)\ge x\) (*)
Thật vậy, (*) \(\Leftrightarrow x^{2022}+3x+16\ge x^{2022}-x^2+11x\)
\(\Leftrightarrow x^2-8x+16\ge0\)
\(\Leftrightarrow\left(x-4\right)^2\ge0\) (luôn đúng)
Vậy \(f\left(x\right)\ge x,\forall x\)
\(\Rightarrow u_{n+1}=f\left(u_n\right)\ge u_n\) nên \(\left(u_n\right)\) là dãy tăng.

Theo t/c CSN \(u_1u_3=u_2^2\Rightarrow u_2^3=64\Rightarrow u_2=4\)
\(\Rightarrow\left\{{}\begin{matrix}u_1+u_3=10\\u_1u_3=16\end{matrix}\right.\)
Theo Viet đảo, \(u_1\) và \(u_3\) là nghiệm: \(t^2-10t+16=0\Rightarrow\left[{}\begin{matrix}t=2\\t=8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}u_1=2\Rightarrow q=2\\u_1=8\Rightarrow q=\frac{1}{2}\end{matrix}\right.\)

1+2+3+4+5+6+7+8+9+10
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11x5
=55
#)Giải :
\(\frac{1}{11}+\frac{2}{11}+\frac{3}{11}+\frac{4}{11}+\frac{5}{11}+\frac{6}{11}+\frac{7}{11}+\frac{8}{11}+\frac{9}{11}+\frac{10}{11}\)
\(=\left(\frac{1}{11}+\frac{10}{11}\right)+\left(\frac{2}{11}+\frac{9}{11}\right)+\left(\frac{3}{11}+\frac{8}{11}\right)+\left(\frac{4}{11}+\frac{7}{11}\right)+\left(\frac{5}{11}+\frac{6}{11}\right)\)
\(=1+1+1+1+1\)
\(=5\)
#~Will~be~Pens~#

2/3 - 1/4 + 5/11
= ( 2/3 - 1/4 ) + 5/11
= (1/3 - 1/2 ) + 5/11
= 5/6 + 5/11
= 85/66
\(\frac{\frac{2}{3}-\frac{1}{4}+\frac{5}{11}}{\frac{5}{12}+1-\frac{7}{11}}\)
\(=\frac{\frac{2}{3}-\frac{1}{4}+\frac{5}{11}}{\frac{5}{12}+1-\frac{7}{11}}\)
\(=\frac{\frac{2}{3}-\frac{1}{4}+\frac{5}{11}}{\frac{103}{132}}\)
\(=\frac{115}{\frac{132}{\frac{103}{132}}}=\frac{115}{132}.\frac{132}{103}\)
\(=\frac{115}{103}\)
Chọn C.
Gọi q là công bội của cấp số. Khi đó ta có:
Suy ra: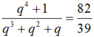 ⇔ 39q4 – 82q3 -82q2 -82q + 39 = 0
⇔ 39q4 – 82q3 -82q2 -82q + 39 = 0
⇔ (3q – 1)(q – 3)(13q2 + 16q + 13) = 0 ⇔ q = 1/3, q = 3