Cho hàm số f x = a x 4 + b x 2 + c với a > 0 , c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x − 2017 là
A. 1
B. 5
C. 3
D. 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:
Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
![]()
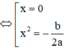
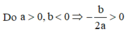
![]()
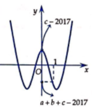
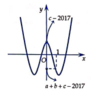
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7

Đáp án D.
Xét hàm số g ( x ) = f ( x ) - 2017 = a x 4 + b x 2 + c - 2017 là hàm trùng phương nên đồ thị hàm số nhận trục Oy làm trục đối xứng và luôn nhận x = 0 là một điểm cực trị.
Ta có g ( 0 ) = c - 2017 > 0 ( d o x > 2017 ) g ( 1 ) = a + b + c - 2107 < 0 ( d o a + b + c < 2017 ) ⇒ g ( 0 ) . g ( 1 ) < 0 ⇒ phương trình g ( x ) = 0 có nghiệm ( 0 ; 1 ) .
Lại có lim x → + ∞ g ( x ) = lim x → + ∞ = x 4 a + b x 2 + c - 2017 x 4 = + ∞ ( d o a > 0 ) nên tồn tại x = x 0 đủ lớn ( x 0 → + ∞ ) sao cho g ( x 0 ) > 0 ⇒ g ( 1 ) . g ( x 0 < 0 ⇒ ) phương trình g ( x ) = 0 có nghiệm trên 1 ; + ∞ .
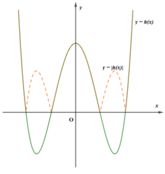
Như vậy, với x > 0 thì phương trình g (x) =0 có ít nhất hai nghiệm nên đồ thị hàm số g (x) cắt Ox tại ít nhất hai điểm nằm bên phải trục tung. Suy ra phương trình g (x) có đúng 4 nghiệm hay đồ thị hàm số g(x) cắt Ox tại đúng 4 điểm và có đồ thị như hình bên. Suy ra hàm số y = g(x) có 3 điểm cực trị (1 cực đại, 2 cực tiểu).
Khi đó hàm số y = g ( x ) có 3 + 4 = 7 điểm cực trị.

Đáp án D

Dựa vào 2 dạng của đồ thị hàm số bậc 4 trùng phương khi a > 0
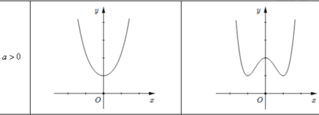
Suy ra hàm số y = f(x) có 3 điểm cực trị và PT: f(x) - 2017 có 4 nghiệm phân biệt
Như vậy PT y ' = 2 f x − 2017 . f ' x 2 f x − 2017 2 = 0 có 7 nghiệm phân biệt do đó hàm số có 7 cực trị.

Bài 2:
Đặt \(2017-x=a;2019-x=b;2x-4036=c\)
\(\Rightarrow a+b+c=0\)
Do \(a+b+c=0\Rightarrow a+b=-c\Leftrightarrow\left(a+b\right)^3=-c^3\)
Có : \(a^3+b^3+c^3=\left(a+b\right)^3-3ab\left(a+b\right)+c^3=-c^3-3ab.\left(-c\right)+c^3=3abc\)
Do \(\left(2017-x\right)^3+\left(2019-x\right)^3+\left(2x-4036\right)^3=0\)
\(\Rightarrow3\left(2017-x\right)\left(2019-x\right)\left(2x-4036\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2017-x=0\\2019-x=0\\2x-4036=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2017\\x=2019\\x=2018\end{matrix}\right.\)

bài 1
ab+bc+ca=0
=>ab+bc=-ca
ta có (a+b)(b+c)(c+a)/abc
=> (ab+ac+bc+b2)(c+a)/abc
=> (0+b2)(c+a)/abc
=>b2c+b2a/abc
=>b(ab+bc)/abc
=>b(-ac)/abc
=>-abc/abc=-1

2.
a. \(A=\left(a+b-c\right)-\left(2a+b-2c\right)\)
\(=a+b-c-2a-b+2c\)
\(=-a+c\)
Thay a=-1 ; c=1 vào A ta có:
\(A=-\left(-1\right)+1=1+1=2\)
Vậy A = 2 với a=-1 ; c = 1
b. \(B=a-\left[\left(a-3\right)+\left(a+3\right)-\left(a-2\right)\right]\)
\(=a-\left(a-3+a+3-a+2\right)\)
\(=a-a+3-a-3+a-2\)
\(=\left(a-a-a+a\right)+\left(3-3-2\right)\)
\(=-2\)
Vậy B = -2