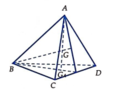
Cho tứ diện ABCD và điểm G thỏa mãn G A → G B → G C → G D → = 0 → (G gọi là trọ...

PT

Pham Trong Bach

12 tháng 12 2019

Cho tứ diện ABCD và điểm G thỏa mãn G A → + G B → + G C → + G D → = 0 → (G gọi là trọng tâm của tứ diện). Gọi G A = G A ∩ B C D . Trong các khẳng định sau, khẳng định nào đúng A. G A → = − 3 G A G → B. ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

12 tháng 12 2019

Đúng(0)

PT

Pham Trong Bach

19 tháng 1 2019

Cho tứ diện ABCD và điểm G thỏa mãn G A ⇀ + G B ⇀ + G C ⇀ + G D ⇀ = 0 ⇀ (G gọi là trọng tâm của tứ diện). Gọi G A = G A ∩ ( B C D ) . Trong các khẳng định sau, khẳng định nào đúng? A. G A ⇀ = ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

19 tháng 1 2019

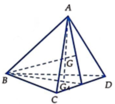
Đáp án C.

+ Gọi G 0 là trọng tâm tam giác BCD=> G B ⇀ + G C ⇀ + G D ⇀ = 3 G G 0 ⇀

=> G A ⇀ + G B ⇀ + G C ⇀ + G D ⇀ = 0 ⇀

=> A, G, G 0 thẳng hàng ⇒ G 0 = G A

+ Có A, G, G A thẳng hàng mà

Đúng(0)

TD

Tử Dương

30 tháng 11 2021

Cho tứ diện ABCD. gọi G₁, G₂ là trọng tâm ∆ABD và ∆ACD. C/m: G₁ G₂ // (ABC) G₁ G₂ // (BCD)

#Toán lớp 11

1

HP

Hồng Phúc

3 tháng 12 2021

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

25 tháng 9 2023

Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $. Chứng minh ba điểm I, G, J thẳng hàng.

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

25 tháng 9 2023

Ta có:

$\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {GI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JD} } \right) = \overrightarrow 0 $

$ \Leftrightarrow 2\overrightarrow {GI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ} + \left( {\overrightarrow {JC} + \overrightarrow {JD} } \right) = \overrightarrow 0 $

$ \Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow 2\left( {\overrightarrow {GI} + \overrightarrow {GJ} } \right) = \overrightarrow 0 $

$ \Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Rightarrow $G là trung điểm của đoạn thẳng IJ

Vậy I, G, J thẳng hàng

Đúng(1)

PT

Pham Trong Bach

4 tháng 8 2018

Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄. A. 2 4 B. 2 18 C. 9 2 32 D. 2 12 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

4 tháng 8 2018

Chọn D

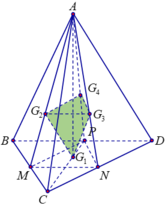
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D

Ta có ngay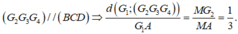

Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3

Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1

Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1

Đúng(0)

HH

Hà Hồng Anh

30 tháng 8 2018 - olm

Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào hình thang ABCD; Gọi A',B',C',D',G' lần lượt là hình chiếu của A,B,C,D,G lên đường thẳng m. Chứng minh GG'=1/4 (AA' +BB' +CC' +DD')

#Toán lớp 8

0

HH

Hà Hồng Anh

30 tháng 8 2018 - olm

Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào hình thang ABCD; Gọi A',B',C',D',G' lần lượt là hình chiếu của A,B,C,D,G lên đường thẳng m. Chứng minh GG'=1/4 (AA' BB' CC' DD')

#Toán lớp 8

0

PT

Pham Trong Bach

16 tháng 2 2017

Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào của hình thang ABCD; Gọi A', B', C’, D’, G' lần lượt là hình chiếu của A, B, C, D, G lên đường thẳng m. Chứng minh GG' =...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

16 tháng 2 2017

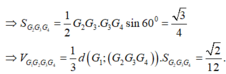
Gọi E và F lần lượt là trung điểm của AC và BD; E' và F' lần lượt là hình chiếu của E, F trên đường thẳng m.

Khi đó, GG' là đường trung bình của hình thang EE'F'F

⇒ G G ' = 1 2 EE' +FF').

Mà EE' và FF' lần lượt là đường trung bình của hình thang AA'C'C và BB'D'D.

⇒ EE ' = 1 2 (AA' +CC') và FF ' = 1 2 (BB' +DD')

Thay vào (1) ta được ĐPCM

Đúng(0)

TD

Thầy Đức Anh

Giáo viên VIP

5 tháng 12 2021 - olm

Cho tứ diện ABCD. Trên cạnh AB lấy điểm M thỏa mãn AM= $\frac{1}{4}$ AB, G là trọng tâm tam giác BCD. Tìm:

a. Giao điểm của GD với (ABC).

b. Giao điểm của MG với (ACD).

#Toán lớp 11

0

TD

Thầy Đức Anh

Giáo viên VIP

5 tháng 12 2021 - olm

Cho tứ diện ABCD. trên cạnh AB lấy điểm M thỏa mãn AM=$\frac{1}{4}$ AB, G là trọng tâm tam giác BCD. Tìm:

a. Giao điểm của GD và (ABC);

b. Giao điểm của MG với (ACD).

#Toán lớp 11

44

NS

Ngô Sỹ Minh

8 tháng 12 2021

Trong (BCD): DG $\cap$ BC = F

Vậy DG $\cap$ (ABC) = F.

b. Cách 1: MG $\subset$ (BMG) $\equiv$ (ABH) (H = BG $\cap$ DC)

(Do mặt phẳng (BMG) "lơ lửng" trong hình chóp nên ta kéo dài BM thành BA và BG thành BH để ta có cái nhìn dễ dàng hơn đối với mặt phẳng này).

(BMG) $\cap$ (ACD) =AH

Trong (ABH): MG $\cap$ AH =K

Vậy MG $\cap$ (ACD) = K.

Đúng(0)

NT

Nguyễn Thị Tâm

8 tháng 12 2021

a. Trong (BCD) có GD và BC cắt nhau tại K

vậy K = GD và (ABC)

b. có MG ⊂ (BMG) trùng (ABH) có H = BG và DC

(BMG) và (ACD) = AH

Trong (ABH) có MG và AH = P

Vậy MG và (ACD) = P

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP