Cho tam giác ABC có hai đường cao AH, BK cắt nhau tại điểm M. Biết
∠ A = 55 o , ∠ B = 67 o
b. Tính (AMB)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
\(\widehat{MBA}=90^0-55^0=35^0\)
\(\widehat{MAB}=90^0-67^0=23^0\)
Do đó: \(\widehat{AMB}=122^0\)
CM
21 tháng 4 2018
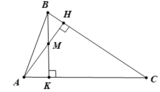
b Trong tam giác vuông ABK có ∠(ABK) + ∠(AKB) + ∠(BAK) = 180o
Nên ∠(ABK) = 180o - 55o - 90o = 35o ( 1 điểm)
Trong tam giác vuông ABH có ∠(BAH) + ∠(ABH) + ∠(BHA) = 180o
Nên ∠(BAH) = 180o - 67o - 90o = 23o ( 1 điểm)
Trong tam giác ABM có ∠(ABM) + ∠(BAM) + ∠(MAB) = 180o nên
∠(AMB) = 180o - 23o - 35o = 122o ( 1 điểm)
CM
5 tháng 7 2018
Để tính góc AMB, ta cần tính ∠A1, ∠B1
Trong tam giác vuông AHB có ∠A1= 90o − ∠(ABH) = 90o − 67 o = 23 o
Trong tam giác vuông AKB có ∠B1= 90o − ∠(BAK) = 90 o − 55o = 35o
Vậy trong tam giác AMB có
∠(AMB) = 180o − (∠A1+ ∠B1) = 180o − (23o + 35o) = 122o.
CM
9 tháng 10 2017
a. Hình vẽ ( 1 điểm)
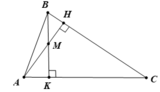
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)
CM
10 tháng 1 2017
a. Hình vẽ ( 1 điểm)
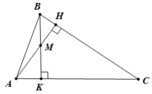
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)
b Trong tam giác vuông ABK có ∠(ABK) + ∠(AKB) + ∠(BAK) = 180o
Nên ∠(ABK) = 180o - 55o - 90o = 35o ( 1 điểm)
Trong tam giác vuông ABH có ∠(BAH) + ∠(ABH) + ∠(BHA) = 180o
Nên ∠(BAH) = 180o - 67o - 90o = 23o ( 1 điểm)
Trong tam giác ABM có ∠(ABM) + ∠(BAM) + ∠(MAB) = 180o nên
∠(AMB) = 180o - 23o - 35o = 122o ( 1 điểm)