B. Phần tự luận (6 điểm)
Cho tam giác MNP có hai đường cao MQ và NH cắt nhau tại I. Biết ( M I N ) = 120 o
a. Tính (MPN)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Hình vẽ ( 1 điểm)
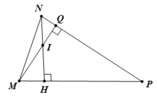
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)

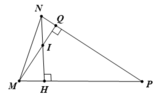
b. Với ∠(MPQ) = 60o, ∠(NMP) = 60o thì tam giác MNP cân tại N và có 1 góc bẳng 60o nên tam giác ABC là tam giác đều ( 1 điểm)
Suy ra AB = BC = AC ( 1 điểm)

b. Với ∠(MPQ) = 60o, ∠(NMP) = 60o thì tam giác MNP cân tại N và có 1 góc bẳng 60o nên tam giác ABC là tam giác đều ( 1 điểm)
Suy ra AB = BC = AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)
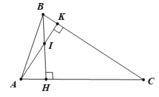
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)

Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)
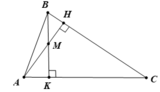
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)
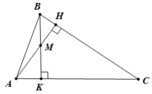
Vì ∠A = 55o, ∠B = 67o nên ∠C = 180o - 55o - 67o = 58o
Vì A < C < B ⇒ BC < AB < AC ( 1 điểm)

a. Hình vẽ ( 0.5 điểm )
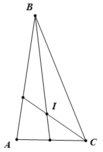
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )
a. Hình vẽ ( 1 điểm)
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)