Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.
A. V = 11 a 3 4
B. V = 11 a 3 6
C. V = 11 a 3 12
D. V = 13 a 3 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 4 2019
Chọn D.
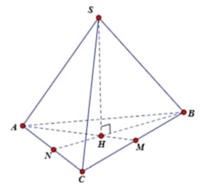
+) Gọi N là trung điểm của AC và H là tâm của ∆ ABC
⇒ B H = 2 3 B N = 2 3 . a 3 2 = a 3 3
+) Có SH ⊥ (ABC) => ∆ SHB vuông tại H
⇒ S H = S B 2 - B H 2 = 21 a 2 36 - a 2 3 = a 2
+) Lại có S A B C = a 2 3 4 (vì ∆ ABC đều có cạnh là a)
V S . A B C D = 1 3 . a 2 . a 2 3 4 = a 3 3 24
CM
20 tháng 11 2017
Chọn B
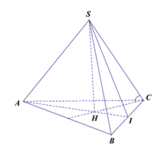
Gọi H là trọng tâm tam giác ABC, khi đó
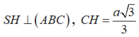
Góc giữa cạnh bên và mặt đáy là góc
CM
31 tháng 7 2018
Đáp án B
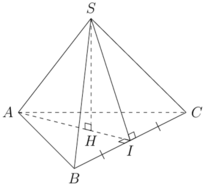
Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó:
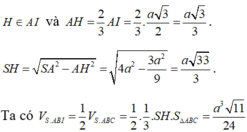
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra S I ⊥ ( A B C )
Gọi M là trung điểm của BC
Diện tích tam giác ABC là: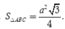
Vậy thể tích khối chóp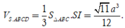
Chọn C.