OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tập huấn miễn phí ra đề kiểm tra và chấm phiếu trắc nghiệm dành cho giáo viên khối THCS

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
2 tháng 9 2017
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn  5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0 A. m > 7 3 B.  - 3 < ...
Đọc tiếp

Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn  5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0

A. m > 7 3

B.  - 3 < m < 7 3

C. - 3 ≤ m ≤ 7 3

D. m < - 3

#Mẫu giáo
1
CM
Cao Minh Tâm
2 tháng 9 2017

Đáp án đúng : C

Đúng(0)
PT
Pham Trong Bach
28 tháng 4 2019
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn  5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0 A. m > 7 3 B.  - 3 < ...
Đọc tiếp

Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có nghiệm thực trong đoạn  5 4 ; 4 m - 1 + log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0

A. m > 7 3

B.  - 3 < m < 7 3

C. - 3 ≤ m ≤ 7 3

D. m < - 3

#Mẫu giáo
1
CM
Cao Minh Tâm
28 tháng 4 2019

Đáp án đúng : C

Đúng(0)
PT
Pham Trong Bach
5 tháng 5 2017
Tập hợp tất cả các giá trị của tham số m để phương trình m - 1 x 2 + 2 x - 3 = 0  có hai nghiệm phân biệt là A.  ℝ = - 1 B.  2 3 ; + ∞ C.  - ∞ ; 2 3 D.  2 3 ; 1 ∪ 1 ; + ∞ ...
Đọc tiếp

Tập hợp tất cả các giá trị của tham số m để phương trình m - 1 x 2 + 2 x - 3 = 0  có hai nghiệm phân biệt là

A.  ℝ = - 1

B.  2 3 ; + ∞

C.  - ∞ ; 2 3

D.  2 3 ; 1 ∪ 1 ; + ∞

#Toán lớp 10
1
CM
Cao Minh Tâm
5 tháng 5 2017

Đúng(0)
PT
Pham Trong Bach
15 tháng 1 2019
Cho bất phương trình x 4   +   x 2   + m 3   -   2 x 2   +   1 3   +   x 2 x 2 - 1   >   1 - m . Tìm tất cả các giá trị thực của tham số m để bất phương trình trên nghiệm đúng ∀ x > 1 . ...
Đọc tiếp

Cho bất phương trình x 4   +   x 2   + m 3   -   2 x 2   +   1 3   +   x 2 x 2 - 1   >   1 - m . Tìm tất cả các giá trị thực của tham số m để bất phương trình trên nghiệm đúng ∀ x > 1 .
#Toán lớp 12
1
CM
Cao Minh Tâm
15 tháng 1 2019

Chọn D

Đúng(0)
PT
Pham Trong Bach
1 tháng 11 2017
Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình x 3 - 3 x 2 + 2   =   m   có nhiều nghiệm thực nhất A. m> -2 B. m> 0 C. -2< m< 2. D. m<...
Đọc tiếp

Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình x 3 - 3 x 2 + 2   =   m   có nhiều nghiệm thực nhất

A. m> -2

B. m> 0

C. -2< m< 2.

D. m< 2.
#Toán lớp 12
1
CM
Cao Minh Tâm
1 tháng 11 2017

+ Ta có hàm số g(x) = x 3   - 3 x 2   + 2   =   m  là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng.

 

+ Khi x≥ 0 ; g(x) = x3- 3x2+ 2

Do đó; đồ thị hàm số g(x) = x 3   -   3 x 2   +   2  có dạng như hình vẽ.

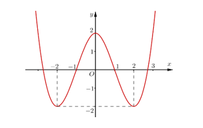
+ Dựa vào đồ thị suy ra phương trình x 3   -   3 x 2   + 2   =   m  có nhiều nghiệm thực nhất khi và chỉ khi -2< m<  2.

Chọn C.

Đúng(0)
PT
Pham Trong Bach
29 tháng 4 2019
Tìm tất cả các giá trị thực của tham số m để hàm số y = log 2 log 5 m - 2 2 + 2 m - 3 x + m  có tập xác định là ℝ. A.  m≤ 7/3. B.  m >7/3. C.  m ≥7/3. D.  m<...
Đọc tiếp

Tìm tất cả các giá trị thực của tham số m để hàm số y = log 2 log 5 m - 2 2 + 2 m - 3 x + m  có tập xác định là ℝ.

A.  m≤ 7/3.

B.  m >7/3.

C.  m ≥7/3.

D.  m< 7/3.
#Mẫu giáo
1
CM
Cao Minh Tâm
29 tháng 4 2019

Đáp án B

Đúng(0)
PT
Pham Trong Bach
5 tháng 11 2017
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên. A. 1 B. 0 C. 2 D....
Đọc tiếp

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.

A. 1

B. 0

C. 2

D. 4
#Toán lớp 12
1
CM
Cao Minh Tâm
5 tháng 11 2017

Đúng(0)
PT
Pham Trong Bach
1 tháng 8 2018

Tập tất cả các giá trị của tham số m để bất phương trình m 2 + 3 m x ≤ m 2  vô nghiệm là:

A. (-3;0)

B. {-3;0}

C.  ∅

D.  - ∞ ; 3

#Toán lớp 10
1
CM
Cao Minh Tâm
1 tháng 8 2018

Để xét bất phương trình bậc nhất vô nghiệm hay luôn đúng với mọi x ta chỉ cần xét hệ số a= 0.

* Với m = 0 thì bất phương  trình đã cho trở thành:

        0 x ≤ 0 ( luôn đúng với mọi  x)   ( loại)

* Với m = -3 thì bất phương trình đã cho trở thành:

        0 x ≤ 9   (luôn đúng với mọi  x)   ( loại)

Vậy không có giá trị nào của m để bất phương trình đã cho vô nghiệm

Đúng(0)
PT
Pham Trong Bach
22 tháng 5 2018

Tập tất cả các giá trị của tham số m để bất phương trình m 2 + 3 m x ≤ m 2  nghiệm đúng với mọi x là:

A. (0;1)

B. {0}

C. {0;1}

D. {1}
#Toán lớp 10
1
CM
Cao Minh Tâm
22 tháng 5 2018

* Nếu m= 0 thì bất phương trình đã cho trở  thành: 

0x < 0(  luôn đúng với mọi x).

* Nếu  m= 1 thì bất phương trình đã cho  trở thành:

0x < 1 ( luôn đúng với mọi x)

Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}

Đúng(0)
PT
Pham Trong Bach
23 tháng 2 2019

Tập tất cả các giá trị của tham số m để hệ bất phương trình  2 x - 1 ≥ 3 x - m ≤ 0 có nghiệm duy nhất là

A.  ∅

B.  2

C.  [ 2 ; + ∞ )

D.  ( - ∞ ; 2 ]

#Toán lớp 10
1
CM
Cao Minh Tâm
23 tháng 2 2019

Ta có  2 x - 1 ≥ 3 x - m ≤ 0 ⇔ x ≥ 2 x ≤ m . Hệ có nghiệm duy nhất khi và chỉ khi m = 2

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP