Hai chất điểm chuyển động với vận tốc có độ lớn là v1 và v2 không đổi. Vận tốc tương đối giữa chúng có giá trị lớn nhất nếu góc hợp bởi v 1 → và v 2 → bằng
A. 00
B. 450
C. 900
D. 1800
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo tính chất của và chạm thì: v → 1 ≠ v → 1 / , v → 2 ≠ v → 2 /
Theo phương ngang động lượng của hệ được bảo toàn nên ta có:
m 1 v 1 / + m 2 v 2 / = m 1 v 1 + m 2 v 2 (1)
Động năng của hệ được bảo toàn:
m 1 v 1 / 2 2 + m 2 v 2 / 2 2 = m 1 v 1 2 2 + m 2 v 2 2 2 (2)
Từ (1) ⇒ m 1 ( v 1 − v 1 / ) = m 2 ( v 2 / − v 2 ) (3)
Từ (2) ⇒ m 1 ( v 1 2 − v 1 / 2 ) = m 2 ( v 2 / 2 − v 2 2 ) (4)
Chia (4) cho (3) vế theo vế ta được: v 1 + v 1 / = v 2 / + v 2 (5)
Từ (5) ⇒ v 2 / = v 1 + v 1 / − v 2 (6)
Thay (6) vào (3) ta được:
v 1 / = ( m 1 − m 2 ) v 1 + 2 m 2 v 2 m 1 + m 2 ; v 2 / = ( m 2 − m 1 ) v 2 + 2 m 1 v 1 m 1 + m 2


+ Tại thời điểm t, dao động thứ nhất có li độ x1 và vận tốc v1, dao động thứ hai chậm pha hơn dao động thứ nhất một góc 0,5π. Biễu diễn các vị trí tương ứng trên đường tròn.
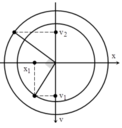
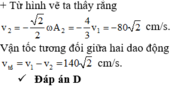

ta có:
t1=\(\frac{S_1}{v_1}=\frac{S}{2v_1}\)
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của nhười đó là:
\(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2v_1}+\frac{S}{2v_2}}=\frac{1}{\frac{1}{2v_1}+\frac{1}{2v_2}}=\frac{1}{\frac{v_2+v_1}{2v_1v_2}}=\frac{2v_1v_2}{v_2+v_1}\)
lấy vtb-trung bình cộng 2 v ta có:
\(\frac{2v_1v_2}{v_1+v_2}-\frac{v_1+v_2}{2}=\frac{4v_1v_2-v_1^2-2v_1v_2-v_2^2}{2\left(v_1+v_2\right)}=\frac{-\left(v_1^2-2v_1v_2+v_2^2\right)}{2\left(v_1+v_2\right)}\)
\(=\frac{-\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)}\)
mà (v1-v2)2>0 nên
-(v1-v2)2<0 và 2*(v2+v1)>0 nên ta suy ra
vận tốc trung bình này ko bao giờ lớn hơn trung bình cộng của hai vận tốc v1 và v2
Đáp án D
v12 lớn nhất bằng |v1 + v2| khi góc hợp bởi v 1 → và v 2 → bằng 1800
Chú ý: v12 lớn nhất bằng |v1 + v2| khi góc hợp bởi v 1 → và v 2 → bằng 1800
v12 nhỏ nhất bằng |v1 - v2| khi góc hợp bởi v 1 → và v 2 → bằng 00