Cho hàm số y = f x = x + 3 m - 2 y. Tất cả các giá trị của tham số m sao cho f x ≥ 0 , ∀ x ∈ [ 1 ; + ∞ ) là
A. m ≤ 1 3
B. m ≤ 2 3
C. m ≥ 1 3
D. 0 < m ≤ 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số y = ax + b ( a ≠ 0 ) đồng biến trên R khi a> 0.
Do đó, để hàm số đã cho đồng biến trên R thì m 2 - 1 > 0 ⇔ [ m > 1 m < - 1
Chọn C.

Đáp án C
Đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
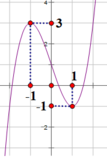
Từ đồ thị hàm số y = x 3 - 3 x + 1 suy ra đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
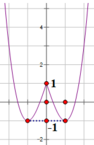
Dựa vào đồ thị hàm số y = x 3 - 3 x + 1 và đồ thị hàm số y = 2 m - 1
Ta có: đường thẳng y = 2 m - 1 cắt đồ thị hàm số y = x 3 - 3 x + 1 tại 4 điểm phân biệt
⇔ - 1 < 2 m - 1 < 1 ⇔ 0 < m < 1

+ Xét hàm số f( x) = x3- x2+ ( m2+ 1) x- 4m- 7 trên đoạn [ 0; 2]
Ta có f’ (x) = 3x2- 2x+ m2+ 1= 3( x-1/3) 2+ m2+ 2/3> 0 .
+ Suy ra hàm số f(x) đồng biến trên
0 ; 2 ⇒ m i n [ 0 ; 2 ] f ( x ) = f ( 0 ) = - 4 m - 7 m a x [ 0 ; 2 ] f ( x ) = f ( 2 ) = 2 m 2 - 4 m - 1
+ Khi đó
m a x [ 0 ; 2 ] y = m a x [ 0 ; 2 ] f ( x ) = m a x - 4 m - 7 ; 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 4 m - 7 ≤ 15 2 m 2 - 4 m - 1 ≤ 15 ⇔ - 11 2 ≤ m ≤ 2 2 m 2 - 4 m - 16 ≤ 0 ⇔ - 11 2 ≤ m ≤ 2 - 2 ≤ m ≤ 4 ⇔ - 2 ≤ m ≤ 2 → m ∈ ℤ m ∈ ± 2 ; ± 1 ; 0
Vậy có 5 giá trị thoả mãn.
Chọn C.
Ta có f x ≥ 0 ⇔ x + 3 m ≥ 2 ⇔ x ≥ 2 - 3 m
f x ≥ 0 với mọi x ∈ [ 1 ; + ∞ ) ⇔ [ 1 ; + ∞ ) ⊂ [ 2 - 3 m ; + ∞ ) ⇔ 2 - 3 m ≤ 1 ⇔ m ≥ 1 3 .
Chọn C.