Cho đường tròn (O) đường kính AB và một cung AC có số đo nhỏ hơn 90 ° . Vẽ dây CD vuông góc với AB và dây DE song song với AB . Chọn kết luận sai?
A. AC = BE
B. Số đo cung AD bằng số đo cung BE
C. Số đo cung AC bằng số đo cung BE
D. A O C ^ < A O D ^





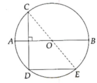
Chọn đáp án D