Một hình cầu có diện tích mặt cầu là 100π ( c m 2 ). Thể tích của hình cầu đó là:
A. 200π ( c m 3 )
B. 250π ( c m 3 )
C. 500π/3 ( c m 3 )
D. 300π ( c m 3 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích bề mặt là `100π => 4π r^2 = 100π => r = 5 (m)`
Thể tích của hình cầu là:
`V=4/3 . π . r^3 = 4/3 . π . 5^3 =500/3 π (m^3)`

a, Tính được S = 64π c m 2 và V = 256 π 3 c m 3
b, Tính được S = 211,32π c m 2

Đáp án D
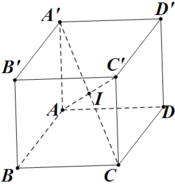
Gọi I là giao điểm các đường chéo của hình hộp thì là tâm mặt cầu cần tìm.
Bán kính mặt cầu là
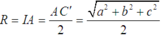
Vậy diện tích của mặt cầu đó là
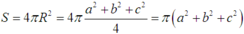

Đáp án D
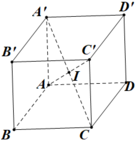
Gọi I là giao điểm các đường chéo của hình hộp thì I là tâm mặt cầu cần tìm.
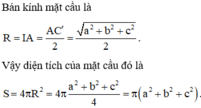

Một hình cầu có số đo diện tích (đơn vị: m2) bằng số đo thể tích (đơn vị: m3). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.
Hướng dẫn làm bài:
Gọi R là bán kính hình cầu (đơn vị : mét)
Khi đó ta có: S = 4πR2 và V=4/3 πR3
Theo đề bài ta có: 4πR2=4/3πR3⇒R/3=1⇒R=3(m)
Ta có: S = 4πR2 = 4π . 32 = 36π (m2)
V=4/3 π R3=4/3 π.33=36π(m3)

Mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật có tâm là tâm của hình hộp chữ nhật đó và có bán kính bằng nửa độ dài đường chéo của hình hộp
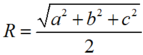
Diện tích của hình cầu đó là:
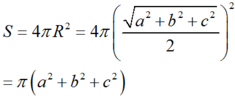
Chọn: C

Chọn A.
Tâm của mặt cầu chính là tâm của của hình hộp chữ nhật.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật.
Mà độ dài đường chéo của hình chữ nhật là ![]() nên mặt cầu (S) có bán kính
nên mặt cầu (S) có bán kính
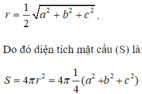
![]()

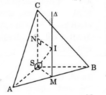
* Gọi M là trung điểm của tam giác SAB.
Tam giác SAB là tam giác vuông tại S có SM là đường trung tuyến nên ta có:
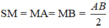
⇒ M là tâm đường tròn ngoại tiếp tam giác SAB.
* Kẻ Mt ⊥ (SAB), ta có: Mt// SC và Mt là trục đưởng tròn ngoại tiếp tam giác SAB.
Trong mp(Mt, SC), đường trung trực của SC cắt Mt tại điểm I.
Ta có: IS = IC. (1)
Và IS = IB = IA (2).
Từ (1) và (2) suy ra: IA = IB= IC = IS
Do đó, I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
Bán kính mặt cầu ngoại tiếp hình chóp là :


Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
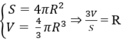
Đáp án là C