Trên cùng một nửa mặt phẳng bờ Ox, vẽ các tia Oy, Oz sao cho ∠xOy= 60 0 , ∠xOz= 120 0
a) Chứng minh rằng Oy là tia phân giác của góc xOz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 9 2018
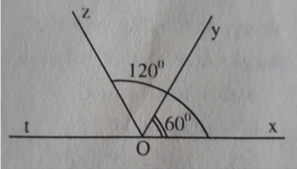
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz và x O y ^ < x O z ^ ( vì 60 ° < 120 ° ) nên tia Oy nằm giữa hai tia Ox, Oz
Ta có:
x O y ^ + y O z ^ = x O z ^
60 ° + y O z ^ = 120 °
y O z ^ = 120 ° - 60 ° = 60 °
Tia Oy nằm giữa hai tia Ox, Oz và x O y ^ = y O z ^ ( = 60 ° )
Vậy tia Oy là phân giác của góc xOz
b) Hai góc xOz và zOt kề bù , nên: x O z ^ + z O t ^ = 180 °
120 ° + z O t ^ = 180 °
z O t ^ = 180 ° - 120 ° = 60 °
Tia Oz nằm giữa hai tia Oy, Ot và y O z ^ = z O t ^ ( = 60 ° )
Vậy tia Oz là phân giác của góc yOt
13 tháng 3 2018
a, vì góc xoy < xoz (60<120)
=>xoy +yoz=xozneen tia oy nam giua 2tia ox và oz
vì tia oy mằm giua 2 tia ox va oz
=> xoy +yoz=xoz
60 độ +yoz=120độ
yoz=120-60=60độ
vì xoy=yoz =1/2 xoz
=> tia oy la tia phan giac cua goc xoz
k nha dung 100%
CM
8 tháng 10 2018
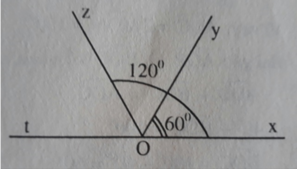
b) Hai góc ∠xOz và ∠zOt kề bù , nên: ∠xOz + ∠zOt = 180 0
120 0 + ∠zOt = 180 0
∠zOt = 180 0 - 120 0 = 60 0
Tia Oz nằm giữa hai tia Oy, Ot và ∠yOz = ∠zOt ( = 60 0 )
Vậy tia Oz là phân giác của góc ∠yOt
24 tháng 3 2021
a) Ta có: \(\widehat{xOy}+\widehat{yOz}+\widehat{xOz}=360^0\)
\(\Leftrightarrow120^0+120^0+\widehat{yOz}=360^0\)
hay \(\widehat{yOz}=120^0\)
\(\Leftrightarrow\widehat{xOy}=\widehat{yOz}=\widehat{xOz}\)(đpcm)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có hai tia Oy, Oz và xOy < xOz ( vì 60 0 < 120 0 ) nên tia Oy nằm giữa hai tia Ox, Oz
Ta có:
∠xOy + ∠yOz = ∠xOz
60 0 + ∠yOz = 120 0
∠yOz = 120 0 - 60 0 = 60 0
Tia Oy nằm giữa hai tia Ox, Oz và ∠xOy = ∠yOz ( = 60 0 )
Vậy tia Oy là phân giác của góc ∠xOz