Thực hiện phép cộng: 1 1 - x + 1 1 + x + 2 1 + x 2 + 4 1 + x 2 + 8 1 + x 2 + 16 1 + x 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

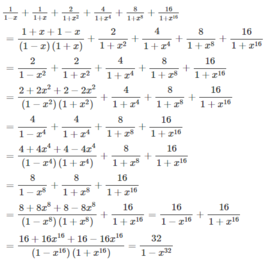

\(A=\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(A=\left(\dfrac{1+x}{\left(1-x\right)\left(1+x\right)}+\dfrac{1-x}{\left(1+x\right)\left(1-x\right)}\right)+...+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{1+x+1-x}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
Tiếp tục các bước như ở dòng 2 và 3 ta có :
\(A=\dfrac{16}{1-x^{16}}+\dfrac{16}{1+x^{16}}\)
\(A=\dfrac{16\left(1+x^{16}\right)}{\left(1-x^{16}\right)\left(1+x^{16}\right)}+\dfrac{16\left(1-x^{16}\right)}{\left(1+x^{16}\right)\left(1-x^{16}\right)}\)
\(A=\dfrac{16+16x^{16}+16-16x^{16}}{1-x^{32}}\)
\(A=\dfrac{32}{1-x^{32}}\)

`a, a/(a-3) - 3/(a+3) = (a(a+3) - 3(a-3))/(a^2-9)`
`= (a^2+9)/(a^2-9)`
`b, 1/(2x) + 2/x^2 = x/(2x^2) + 4/(2x^2) = (x+4)/(2x^2)`
`c, 4/(x^2-1) - 2/(x^2+x) = (4x)/(x(x-1)(x+1)) - (2(x-1))/(x(x+1)(x-1))`
`= (2x+2)/(x(x-1)(x+1)`
`= 2/(x(x-1))`

ĐKXĐ\(\begin{cases}x^2-4\ne0\\x+2\ne0\\2-x\ne0\end{cases}\)<=>\(\begin{cases}x\ne-2\\x\ne2\end{cases}\)
Với \(x\ne-2,x\ne2\) ta có
\(\frac{x^2}{x^2-4}+\frac{1}{x+2}+\frac{2}{2-x}\)=\(\frac{x^2}{\left(x+2\right)\left(x-2\right)}+\frac{1}{x+2}-\frac{2}{x-2}\)
=\(\frac{x^2}{\left(x+2\right)\left(x-2\right)}+\frac{x-2}{\left(x+2\right)\left(x-2\right)}-\frac{2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\)
=\(\frac{x^2+x-2-2x-4}{\left(x+2\right)\left(x-2\right)}\)=\(\frac{x^2-x+6}{\left(x+2\right)\left(x-2\right)}\)
=\(\frac{\left(x+2\right)\left(x-3\right)}{\left(x+2\right)\left(x-2\right)}\)=\(\frac{x-3}{x-2}\)

\(=\dfrac{1+x+1-x}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{2+2x^2+2-2x^2}{1-x^4}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{4}{1-x^4}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{4+4x^4+4-4x^4}{1-x^8}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{8+8x^8+8-8x^8}{1-x^{16}}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{16+16x^{16}+16-16x^{16}}{1-x^{32}}=\dfrac{32}{1-x^{32}}\)


\(=\dfrac{3x^2+5x+14+x^2-1-4x^2+4x-4}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{9x+9}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{9}{x^2-x+1}\)

Câu hỏi của Best Friend Forever - Toán lớp 7 - Học toán với OnlineMath

theo cách tính tổng (bn có thể xem lại ở toán 7 hay 6 j đấy) thì bt trên bằng 1/x - 1/(x+5)
từ đó tính tiếp nha bn

a: \(=\dfrac{3b+4a}{6ab}\)
b: \(=\dfrac{x^2-2x+1-x^2-2x-1}{x^2-1}=\dfrac{-4x}{x^2-1}\)
c: \(=\dfrac{xz+yz-xy-xz}{xyz}=\dfrac{yz-xy}{xyz}=\dfrac{z-x}{xz}\)
d: \(=\dfrac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
e: \(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)