Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đọc mà rối loạn tâm chí, chi co cao thủ như các thầy cô giáo mới làm đc

Xét tam giác DEF có:
M là trung điểm DE
MN//EF
=> N là trung điểm DF
Vậy dự đoán N là trung điểm DF

?4:
Xét ΔADC có
E là trung điểm của AD
EI//DC
Do đó:I là trung điểm của AC
Xét ΔCAB có
I là trung điểm của CA
IF//AB
Do đó: F là trug điểm của BC
?2:
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>góc ADE=góc ABC

xét tứ giác AEDF
DF//AE vì E thuộc AC
ED//AF vì F thuộc AB
=>AEDF là hình bình hành (các cạch đối //)
=>dpcm

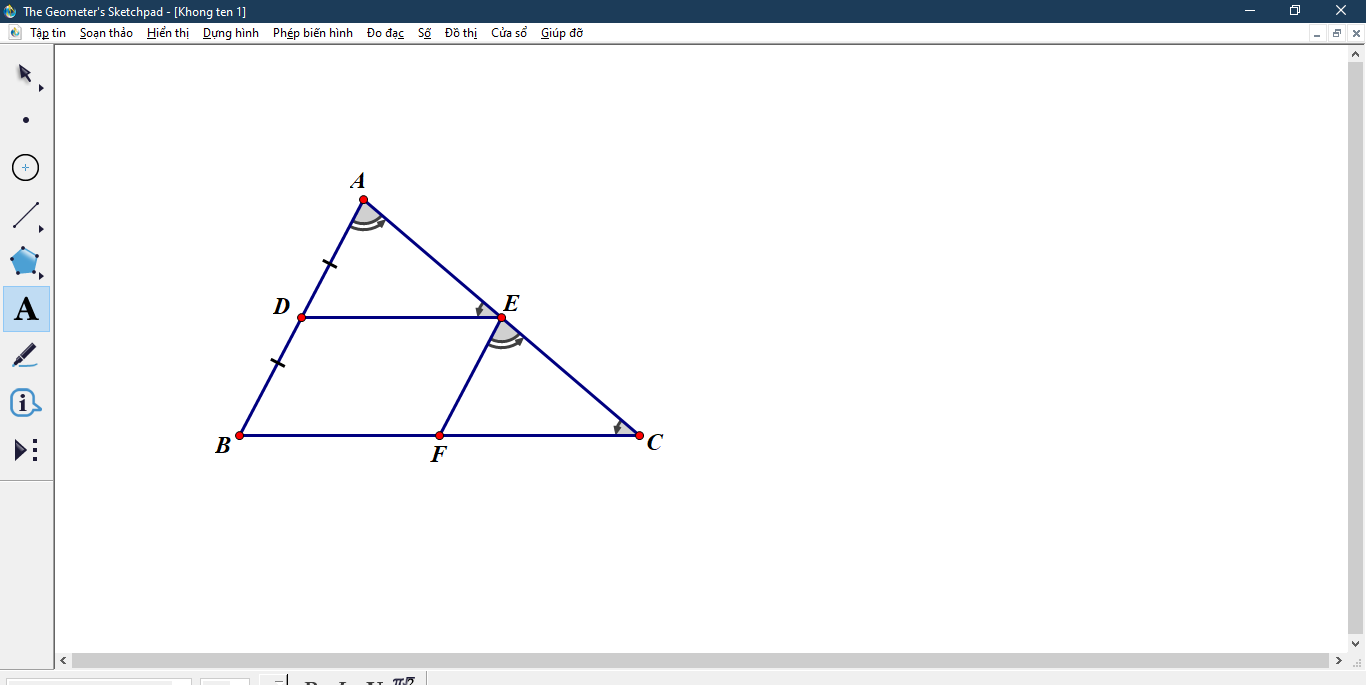
Xét \(\Delta ABC\) có AD=DB;DE//BC nên AE=EC hay E là trung điểm AC
Xét \(\Delta ADE\) và \(\Delta EFC\) có:
\(\left\{{}\begin{matrix}\widehat{DAE}=\widehat{FEC}\\AE=EC\left(cmt\right)\\\widehat{AED}=\widehat{ECF}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ADE\) \(=\) \(\Delta EFC\)\(\left(g.c.g\right)\)
Tick hộ nha
Vì AD=BD và d//BC
=> E là trung điểm của AC
=> AE = EC
Vì DE//BC
=> \(\widehat{AED}=\widehat{ECF}\) (2 góc đồng vị)
Vì ÈF//AB
\(\Rightarrow\widehat{DAE}=\widehat{FEC}\) (2 góc đồng vị)
Xét ΔADE và ΔECF có;
\(\widehat{AED}=\widehat{ECF}\) (cmt)
AE = EC
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=> ΔADE = ΔECF (g-c-g)


Dự đoán: E là trung điểm cạnh AC