Cho ba điểm A, B, C thẳng hàng theo thứ tự đó. Trên nửa mặt phẳng bờ là đường thẳng AC lấy điểm D .Trên nửa mặt phẳng còn lại lấy điểm E. Vẽ tia BD, BE. Gọi tên hai tia đối nhau ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


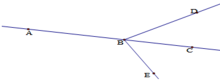
Vì hai điểm D, E thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng AC nên đoạn thẳng DE có cắt đường thẳng AC.

Thứ nhất phải nói, công cụ vẽ hình quá sơ sài :)
a/ cm C, O , D thẳng hàng.
Xét tam giác AOC và tam giác BOD ta có:
AO = OB(O là trung điểm của AB) (1)
AC = BD (gt) (2)
góc CAO = góc DBO (2 góc so le trong , Ax//By) (3)
Từ (1),(2),(3) => tam giác AOC và tam giác BOD (c-g-c)
=> góc AOC = góc BOD (2 góc tương ứng).
Ta có :
góc AOC + góc COD = 1800 (2 góc kề bù) (1)
góc AOC = góc BOD (cmt) (2)
Từ (1),(2) => góc BOD + góc COD = 1800
=> góc COD = 1800
=> C, O , D thẳng hàng.
C/m E,O,F thẳng hàng.
bạn tự chứng minh theo cách trên.
b/ cm DE = CF và DE// CF
Ta có :
AE = BF (gt) (1)
AC = BD (gt) (2)
Từ (1),(2)=> AE - AC = BF - BD
=> CE = DF
Xét tam giác DEC và tam giác CFD ta có:
CD = CD (cạnh chung) (1)
CE = FD (cmt) (2)
góc ECD = góc FDC (2 góc so le trong, Ax//By) (3)
Từ (1),(2),(3) => tam giác DEC = tam giác CFD (c-g-c)
=> DE = CF (2 cạnh tương ứng)
Ta có :
góc CDE = góc DCF ( tam giác DEC = tam giác CFD)
mà góc CDE và góc DCF nằm ở vị trí so le trong
nên DE //CF

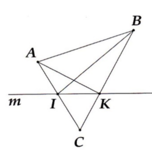
a) Ta suy ra điểm K nằm giữa hai điểm B, C nên tia AK nằm giữa hai tia AB và AC.
Tương tự, ta có điểm I nằm giữa hai điểm A, C nên tia BI nằm giữa, hai tia BA, BC.
b) Từ câu b), ta suy ra tia BI nằm giữa hai tia BA,BK nên tia BI cắt đoạn thẳng AK tại một điểm nằm giữa A và K.
Lập luận tương tự, ta có tia AK cắt đoạn thẳng BI tại một điểm nằm giữa B và I. Từ đó suy ra hai đoạn thẳng AK và BI cắt nhau.
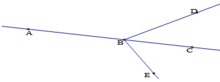

Hai tia đối nhau là BA, BC.