So sánh hai phân số : - 2 3 v à 4 - 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

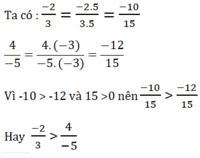

1.a) 3/4 > 5/10
b) 35/25 > 16/14
2.a) 7/5 > 5/7
b) 14/16 < 24/21
HT nha
( bạn t.i.c.k cho mik nha, mik cảm ơn )

a)
Ta thấy : 23/41 < 1 , 3/2 > 1
=> 23/41 < 3/2
b)
Ta có phân số trung gian là: 15/20
15/23<15/20<17/20
=>15/23 < 17/20

Bài 1: Quy đồng => so sánh => trả về phân số ban đầu
Bài 2: Như bài 1
Bài 1
a) 4/3 < 1/3
b) 2/5 < 3/2
c) 7/2 > 1/4
d) 3/4 < 5/6
Bài 2
a) 6/10 = 3/5 và 4/5 vậy 3/5 < 4/5
b) 3/4 và 6/12 = 1/2 vậy 3/4 > 1/2

1) \(A=\left(\sqrt{7-\sqrt{21}+4\sqrt{5}}\right)^2=7-\sqrt{21}+4\sqrt{5}\)
\(B=\left(\sqrt{5}-1\right)^2=6-2\sqrt{5}\)
\(\Rightarrow A-B=1-\sqrt{21}+6\sqrt{5}=\left(1+\sqrt{180}\right)-\sqrt{21}>0\)
\(\Rightarrow A>B\Rightarrow\sqrt{7-\sqrt{21}+4\sqrt{5}}>\sqrt{5}-1\)
2) \(C=\left(\sqrt{5}+\sqrt{10}+1\right)^2=5+10+1+10\sqrt{2}+2\sqrt{5}+2\sqrt{10}\)
\(=26+10\sqrt{2}+2\sqrt{5}+2\sqrt{10}>26+10>35=\left(\sqrt{35}\right)^2\)
Vậy \(\sqrt{5}+\sqrt{10}+1>\sqrt{35}\)
3) \(\left(\frac{15-2\sqrt{10}}{3}\right)^2=\frac{225-60\sqrt{10}+40}{9}=\frac{265-60\sqrt{10}}{9}=\frac{265}{9}-\frac{20\sqrt{10}}{3}< 15\)
Vậy nên \(\frac{15-2\sqrt{10}}{3}< \sqrt{15}\)

\(\sqrt[3]{\left(1-\sqrt{3}\right)\left(4-2\sqrt{3}\right)}=\sqrt[3]{\left(1-\sqrt{3}\right)\left(\sqrt{3}-1\right)^2}\)=\(\sqrt[3]{\left(1-\sqrt{3}\right)^3}\)=1-\(\sqrt{3}\)
\(\sqrt[3]{\left(1-\sqrt{5}\right)\left(6-2\sqrt{5}\right)}=\sqrt[3]{\left(1-\sqrt{5}\right)\left(\sqrt{5}-1\right)^2}\)=\(\sqrt[3]{\left(1-\sqrt{5}\right)^3}\)=1-\(\sqrt{5}\)
Ta thấy \(\sqrt{5}>\sqrt{3}\)nên 1-\(\sqrt{3}\)>\(1-\sqrt{5}\)
Vậy \(\sqrt[3]{\left(1-\sqrt{3}\right)\left(4-2\sqrt{3}\right)}\)>\(\sqrt[3]{\left(1-\sqrt{5}\right)\left(6-2\sqrt{5}\right)}\)

b) \(\frac{5}{9}\)và \(\frac{5}{8}\) :Quy đồng mẫu số : \(\frac{5}{9}\) = \(\frac{5.8}{9.8}\) = \(\frac{40}{72}\) ; \(\frac{5}{8}\) = \(\frac{5.9}{8.9}\) = \(\frac{45}{72}\)
Vì \(\frac{40}{72}\) < \(\frac{45}{72}\) nên \(\frac{5}{9}\) < \(\frac{5}{8}\)
c)\(\frac{8}{7}\) và \(\frac{7}{8}\) :Quy đồng mẫu số: \(\frac{8}{7}\) = \(\frac{8.8}{7.8}\) = \(\frac{64}{56}\) ; \(\frac{7}{8}\) = \(\frac{7.7}{8.7}\) =\(\frac{49}{56}\)
Vì \(\frac{64}{56}\) > \(\frac{49}{56}\) nên \(\frac{8}{7}\) > \(\frac{7}{8}\)
bạn an đông à cái câu A của bạn sai một chút.
CHÚC BẠN HỌC TỐT !
a)\(\frac{3}{7}\) và\(\frac{2}{8}\) :Quy đồng mẫu số : \(\frac{3}{7}\) = \(\frac{3.8}{7.8}\) = \(\frac{24}{56}\) ; \(\frac{2}{8}\) = \(\frac{2.7}{8.7}\) = \(\frac{14}{56}\)
Vì \(\frac{24}{56}\) > \(\frac{14}{56}\) nên \(\frac{3}{7}\) > \(\frac{2}{8}\)

c) Đặt \(A=2^0+2^1+2^2+...+2^{50}\)
\(\Leftrightarrow2A=2^1+2^2+2^3...+2^{51}\)
\(\Leftrightarrow2A-A=2^1+2^2+2^3...+2^{51}\)\(-2^0-2^1-2^2-...-2^{50}\)
\(\Leftrightarrow A=2^{51}-2^0=2^{51}-1< 2^{51}\)
Vậy \(2^0+2^1+2^2+...+2^{50}< 2^{51}\)
a)Ta có: \(\hept{\begin{cases}2^{30}=\left(2^3\right)^{10}=8^{10}\\3^{30}=\left(3^3\right)^{10}=27^{10}\\4^{30}=\left(2^2\right)^{30}=2^{60}\end{cases}}\)và \(\hept{\begin{cases}3^{20}=\left(3^2\right)^{10}=9^{10}\\6^{20}=\left(6^2\right)^{10}=36^{10}\\8^{20}=\left(2^3\right)^{20}=2^{60}\end{cases}}\)
Mà \(8^{10}< 9^{10}\); \(27^{10}< 36^{10}\);\(2^{60}=2^{60}\)nên
\(8^{10}+27^{10}+2^{60}< 9^{10}+36^{10}+2^{60}\)
hay \(2^{30}+3^{30}+4^{30}< 3^{20}+6^{20}+8^{20}\)

a)Ta có :\(3^{60}=\left(3^3\right)^{20}=27^{20}\)
\(2^{80}=\left(2^4\right)^{20}=16^{20}\)
Mà \(27^{20}>16^{20}\Leftrightarrow3^{60}>2^{80}\)
b)Ta có :\(5^{20}=\left(5^4\right)^5=625^5\)
\(4^{25}=\left(4^5\right)^5=1024^5\)
Mà \(1024^5>625^5\Leftrightarrow5^{20}< 4^{25}\)