Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


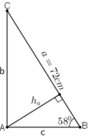
+ Ĉ + B̂ = 90º ⇒ Ĉ = 90º - B̂ = 90º – 58º = 32º
+ b = a.sinB = 72 . sin 58º ≈ 61,06 cm
+ c = a . cos B = 72 . cos 58º ≈ 38,15cm
+ ha = c . sin B = 38,15 . sin 58º = 32,36 cm.

Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).

Theo định lý tổng ba góc trong tam giác ABC, ta có:
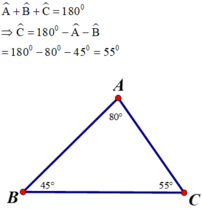
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.

a: XétΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< Â\)
b: \(\widehat{C}=180^0-100^0-30^0=50^0\)
Xét ΔABC có \(\widehat{B}< \widehat{C}< \widehat{A}\)
nên AC<AB<BC
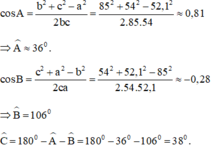
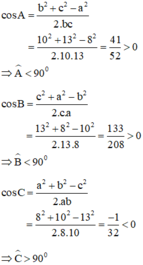
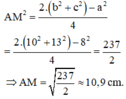
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm