Một thanh AB đồng chất, khối lượng m = 2,0 kg tựa lên hai mặt phẳng nghiêng không ma sát, với các góc nghiêng
α
=
30
°
và
β
=
60
°
. Biết giá của trọng lực của thanh đi qua giao tuyến O của hai mặt phẳng nghiêng (H.17.5). Lấy g = 10 m/
s
2
. Xác định áp lực của thanh lên mỗi mặt phẳng...
Đọc tiếp
Một thanh AB đồng chất, khối lượng m = 2,0 kg tựa lên hai mặt phẳng nghiêng không ma sát, với các góc nghiêng α = 30 ° và β = 60 ° . Biết giá của trọng lực của thanh đi qua giao tuyến O của hai mặt phẳng nghiêng (H.17.5). Lấy g = 10 m/ s 2 . Xác định áp lực của thanh lên mỗi mặt phẳng nghiêng.
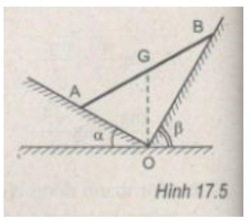
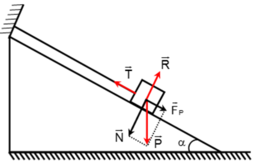
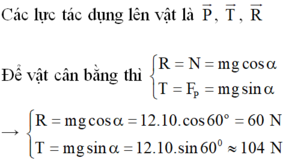
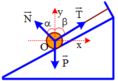
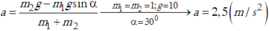
Thanh AB chịu ba lực cân bàng là P → , N 1 → và N 2 → . Vì mặt phẳng nghiêng không ma sát nên hai phản lực N 1 → và N 2 → vuông góc với các mặt phẳng nghiêng. Ta trượt các vectơ lực trên giá của chúng đến điểm đồng quy C (H.17.5G).
Từ tam giác lực, ta được :
N 1 = Psin 30 ° = 20.0,5 = 10 N
N 2 = Pcos 30 ° = 20. 3 /2 = 17,3 ≈ 17 N
Theo định luật III Niu-tơn thì áp lực của thanh lên mặt phẳng nghiêng có độ lớn bằng phản lực của mặt phẳng nghiêng lên thanh.