Tính tổng 3 số nguyên dương x;y;z biết x+y+z=xyz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 3 2022
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
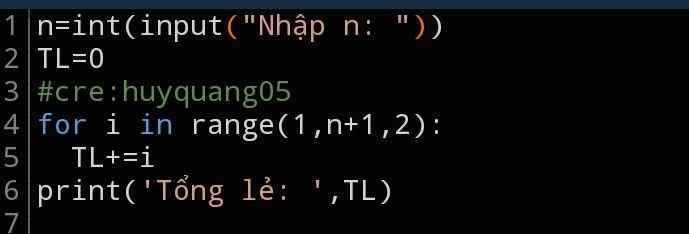
cin>>n;
t=0;
for (i=1; i<=n; i++) if (i%2!=0) t+=i;
cout<<t;
return 0;
}
11 tháng 12 2021
1:
#include <bits/stdc++.h>
using namespace std;
long long n,i,dem,x;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x==0) dem++;
}
cout<<dem;
return 0;
}
7 tháng 11 2021
Câu 1:
#include <bits/stdc++.h>
using namespace std;
long long n;
int main()
{
cin>>n;
int t=0;
while (n>0)
{
int x=n%10;
t=t+x;
n=n/10;
}
cout<<t;
return 0;
}
18 tháng 11 2021
#include<iostream>
using namespace std;
int main() {
int a,b,c;
cin >> a >> b >> c;
cout << a + b +c;
return 0;
}
28 tháng 2 2023
1:
uses crt;
var n,i,t:integer;
begin
clrscr;
readln(n);
t:=0;
for i:=1 to n do
t:=t+i*i;
write(t);
readln;
end.
4 tháng 4 2023
2
program bt2;
var i,n,t:integer;
begin
readln(n);
s:=0;
for i:=1 to n do
if i mod 2 = 1 then s:=s+i;
readln;
end.
AT
1
21 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
long long x,i,n,t,a;
int main()
{
cin>>n>>x;
t=0;
for (i=1; i<=n; i++)
{
cout<<a;
if (a==x) t=t+a;
}
cout<<t;
return 0;
}
CM
2 tháng 4 2019
a) Số nguyên dương nhỏ nhất là 1
Do đó, ta có : x + 2011 = 1
x = 1 – 2011 = -2010
b) Các số nguyên có giá trị tuyệt đối nhỏ hơn 100 là -99 ; -98 ; … ; 98 ; 99
Tổng cần tìm là: ( -99 + 99 ) + ( -98 + 98 ) + … + ( -1 + 1 ) + 0 = 0 + 0 + ... + 0 = 0
H9
HT.Phong (9A5)
CTVHS
26 tháng 9 2023
Số hạt mang điện tích dương là 7 \(\Rightarrow p=7\)
Số hạt không mang điện tích là 7 \(\Rightarrow n=7\)
Mà số hạt mang điện tích dương bằng số hạt mang điện tích âm nên: \(e=p=7\)
Tổng số hạt trong nguyên tử X là:
\(p+e+n=7+7+7=21\) (hạt)
NT
tìm x sao cho x + 2011 là số nguyên dương nhỏ nhất
tính tổng và tích các số nguyên x, biết -567<x<567
1
TN
6 tháng 2 2017
a, Vì x + 2011 là số nguyên dương nhỏ nhất nên x là hiệu của số nguyên dương nhỏ nhất và 2011.
x = 1 - 2011
x = -2010.
b, -567 < x < 567
-566 \(\le x\le566\)
Vậy tổng các số nguyên x là 0.
Tổng 3 số đó là xyz
Do x,y,z có vai trò như nhau nên ta giả sử 0<x≤y≤z
Khi đó ta có xyz=x+y+z < 3z
=> xy < 3
Mà x,y là các số nguyên dương nên xyϵ{1;2;3}
Ta xét các trường hợp
+) TH1: xy=1 =>x=1;y=1=>2+z=z, vô lí
+) TH2: xy=2=>x=1;y=2 (do x<y) >3+z=2z<=>z=3
+) TH3: xy=3=>x=1;y=3=>4+z=3z<=>z=2
Nên ta có các cặp số (x;y;z) thỏa mãn đề bài là các hoán vị của (1;2;3) Khi đó x+y+z=6