Cho đoạn mạch gồm n điện trở R 1 = 1 Ω , R 2 = 1 2 Ω , ... , R n = 1 n Ω mắc song song. Tìm điện trở tương đương của mạch?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có:
U2=I2R2=34.2V
do U1=U2=U3=U nên U=34.2V
ta lại có:
\(I_1=\frac{U_1}{R_1}=1.425A\)
\(I_3=\frac{U_3}{R_3}=0.95A\)
mà I=I1+I2+I3=1.425+0.95+1.9=4.275A

Chọn: C
Hướng dẫn:
- Điện trở mạch ngoài là
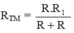
- Xem hướng dẫn câu 2.36: Khi công suất tiêu thụ mạch ngoài lớn nhất thì R TM = r = 2 (Ω).

Đáp án C
Bốn nguồn giống nhau mắc song song nên:
I = ξ b R + r b = ξ R + r 4 = 4,5 2+ 1 4 = 2 A

Chọn: B
Hướng dẫn:
- Đoạn mạch gồm nguồn điện có suất điện động E = 12 (V), điện trở trong r = 3 (Ω), mạch ngoài gồm điện trở R 1 = 6 (Ω) mắc song song với một điện trở R, khi đó mạch điện có thể coi tương đương với một nguồn điện có E = 12 (V), điện trở trong r' = r // R 1 = 2 (Ω), mạch ngoài gồm có R
- Xem hướng dẫn câu 2.36. Công suất tiêu thụ trên R đạt giá trị max khi R = r' = 2 (Ω)

Mắc 4 điện trở 20Ω song song với nhau
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_1}+\dfrac{1}{R_1}+\dfrac{1}{R_1}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1R_1R_1R_1}{R_1R_1R_1+R_1R_1R_1+R_1R_1R_1+R_1R_1R_1}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1^4}{4R_1^3}=\dfrac{20^4}{4.20^3}=5\left(\Omega\right)\)




Hướng dẫn giải
Mạch điện gồm n điện trở ghép nối tiếp nên:
1 R t d = 1 R 1 + 1 R 2 + ... + 1 R n = 1 2 + 2 + 3 + ... + n = n ( n + 1 ) 2 ⇒ R t d = 2 n ( n + 1 ) Ω