Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, Kẻ tiếp tuyến chung ngoài BC, B ϵ (O), C ϵ (O'). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
Chứng minh rằng ∠BAC = 90o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 1 2019
a, Vì AI là tiếp tuyến chung trong
BC là tiếp tuyến chung ngoài
=> IA = IB = IC
=> tam giác BAC vuông ở A
=> ^BAC = 90o
b, Vì IA , IB là tiếp tuyến (O)
=> IO là phân giác ^BIA
=> \(\widehat{OIA}=\frac{\widehat{BIA}}{2}\)
Tương tự \(\widehat{O'IA}=\frac{\widehat{CIA}}{2}\)
Mà \(\widehat{BIA}+\widehat{CIA}=180^o\)
\(\Rightarrow\frac{\widehat{BIA}+\widehat{CIA}}{2}=90^o\)
=> ^OIA + ^O'IA = 90o
=> ^OIO' = 90o
c, Xét tam giác OIO' vuông tại I có IA là đường cao
\(IA^2=OA.O'A\)(Hệ thức lượng)
\(\Leftrightarrow IA^2=9.4\)
\(\Leftrightarrow IA=6\)(Do IA > 0)
MÀ BC = 2IA
=> BC = 12
CM
1 tháng 10 2019
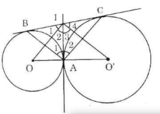
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
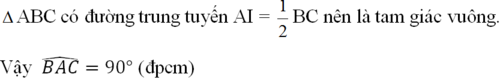
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
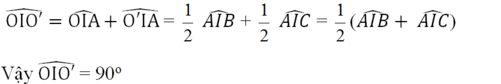
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
CM
6 tháng 1 2018
Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
O I O ' ^ = O I A ^ + O ' I A ^ = 1 2 A I B ^ + 1 2 A I C ^ = 1 2 A I B ^ + A I C ^
Vậy O I O ' ^ = 90 o
CM
6 tháng 2 2017
ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
CM
31 tháng 10 2019
a) Ta có:
IA = IB = IC
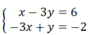
Tam giác BAC có AI là trung tuyến và AI = BC/2
⇒ Tam giác BAC vuông tại A hay ∠BAC = 90 0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
a.
Do IA và IB là tiếp tuyến của (O), theo t/c hai tiếp tuyến cắt nhau ta có: \(IA=IB\)
Tương tự, IA và IC là tiếp tuyến của (O') \(\Rightarrow IA=IC\)
\(\Rightarrow IA=IB=IC=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow\widehat{BAC}=90^0\)
b.
Theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{OIB}=\widehat{OIA}=\dfrac{1}{2}\widehat{BIA}\\\widehat{O'IC}=\widehat{O'IA}=\dfrac{1}{2}\widehat{CIA}\end{matrix}\right.\)
\(\Rightarrow\widehat{OIA}+\widehat{O'IA}=\dfrac{1}{2}\left(\widehat{BIA}+\widehat{CIA}\right)\)
\(\Rightarrow\widehat{OIO'}=\dfrac{1}{2}.\widehat{BIC}=\dfrac{1}{2}.180^0=90^0\)
\(\Rightarrow\Delta OIO'\) vuông tại O
Do IA là tiếp tuyến chung tại điểm tiếp xúc ngoài của 2 đường tròn \(\Rightarrow IA\perp O'O\)
Áp dụng hệ thức lượng trong tam giác vuông OIO' với đường cao IA:
\(IA^2=OA.O'A=36\Rightarrow IA=6\left(cm\right)\)
\(\Rightarrow BC=2IA=12\left(cm\right)\)
Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
tam giác ABC có đường trung tuyến AI = 1/2 BC nên là tam giác vuông
vậy B A C ^ = 90 o