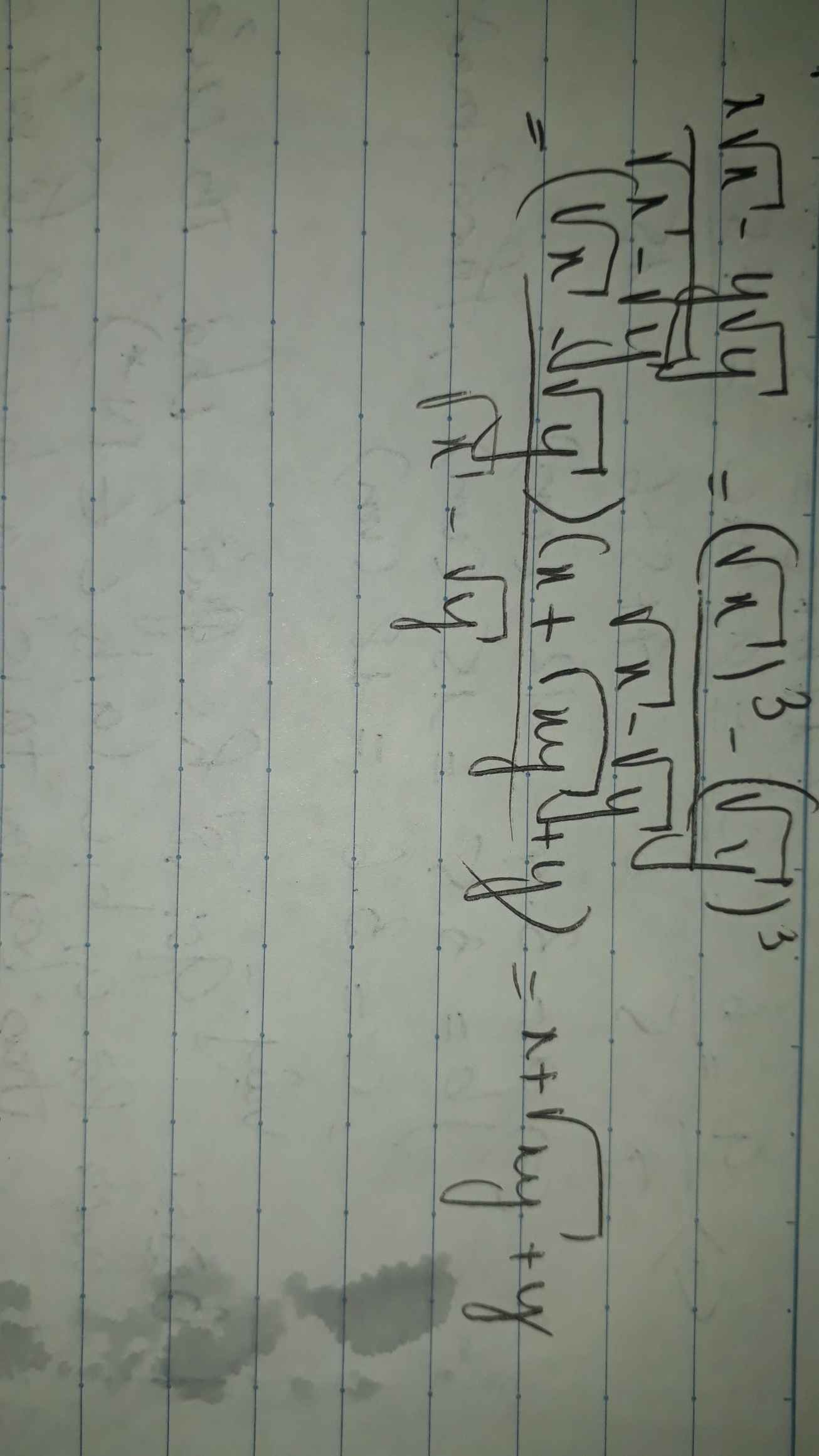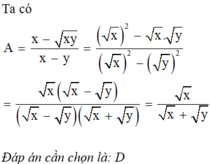Rút gọn: P = x x + y y x + y - x - y 2 với x ≥ 0, y ≥ 0, x 2 + y 2 > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

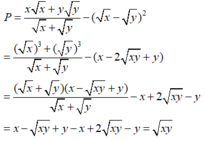

\(\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=x+\sqrt{xy}+y\)

\(=\dfrac{2}{x+y}\cdot\dfrac{\sqrt{3}\left(x+y\right)}{2}=\sqrt{3}\)

3x=2y
nên x/2=y/3
Đặt x/2=y/3=k
=>x=2k; y=3k
\(P=\dfrac{\left(2k\right)^2-2k\cdot3k+\left(3k\right)^2}{\left(2k\right)^2+2k\cdot3k+\left(3k\right)^2}\)
\(=\dfrac{4k^2-6k^2+9k^2}{4k^2+6k^2+9k^2}=\dfrac{4-6+9}{4+6+9}=\dfrac{7}{19}\)

\(A=\dfrac{2x}{x\left(x+y\right)}+\dfrac{6x}{\left(x-y\right)\left(x+y\right)}-\dfrac{3}{x-y}\)
\(=\dfrac{2\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}+\dfrac{6x}{\left(x-y\right)\left(x+y\right)}-\dfrac{3\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{2x-2y+6x-3x-3y}{\left(x-y\right)\left(x+y\right)}=\dfrac{5\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{5}{x+y}\)

\(\dfrac{1}{y-x}\cdot\sqrt{x^6\left(x-y\right)^2}\)
\(\dfrac{1}{y-x}\cdot x^3\cdot\left(x-y\right)\)
\(=-x^3\)

\(=\dfrac{1}{y-x}\cdot x^3\cdot\left(x-y\right)=-x^3\)