Khử mẫu của biểu thức lấy căn
1 600 ; 11 540 ; 3 50 ; 5 98 ; 1 - 3 2 27
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\sqrt{\dfrac{b+1}{b^2}}=\left[{}\begin{matrix}\dfrac{\sqrt{b+1}}{b}\left(b>0\right)\\-\dfrac{\sqrt{b+1}}{b}\left(-1\le b< 0\right)\end{matrix}\right.\)

\(\sqrt{\dfrac{1}{600}}\)=\(\sqrt{\dfrac{1}{10^2\cdot6}}\)=\(\sqrt{\dfrac{1\cdot6}{10^2\cdot6\cdot6}}\)=\(\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}\)=\(\sqrt{\dfrac{11\cdot540}{540\cdot540}}\)=\(\dfrac{\sqrt{5940}}{540}\)=\(\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}\)=\(\sqrt{\dfrac{3\cdot50}{50\cdot50}}\)=\(\dfrac{\sqrt{150}}{50}\)=\(\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}\)=\(\sqrt{\dfrac{5\cdot98}{98\cdot98}}=\dfrac{\sqrt{490}}{98}=\dfrac{\sqrt{10}}{14}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{3-\sqrt{3}}{9}\)
\(\sqrt{\dfrac{1}{600}}=\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}=\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}=\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}=\dfrac{\sqrt{10}}{14}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{3-\sqrt{3}}{9}\)

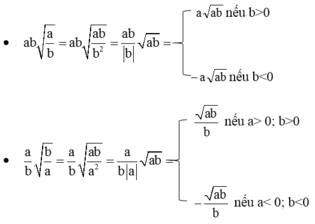
(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)
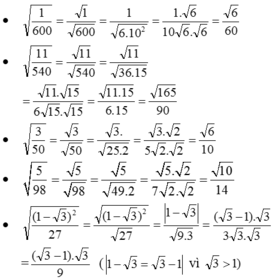

(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)
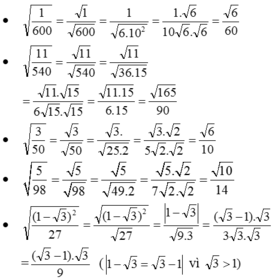

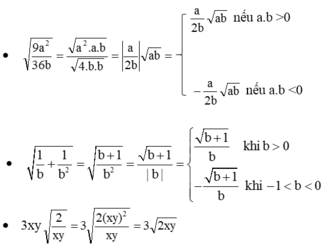
(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)
(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)